| Codeforces Round 459 (Div. 1) |
|---|
| Закончено |
Как мы все знаем, Макс лучше всех играет в компьютерные игры. Ее друзья настолько ей завидуют, что придумали игру в реальном мире, чтобы показать, что она не во всех играх лучшая. Игра проходит на ориентированном ациклическом графе с n вершинами и m ребрами. На каждом ребре написан символ — строчная латинская буква.

Играют Макс и Лукас. Первой ходит Макс, потом ходит Лукас, затем снова Макс и так далее. У каждого игрока есть камешек, изначально расположенный в некоторой вершине. Каждый игрок в свой ход должен передвинуть свой камешек вдоль одного ребра (игрок может передвинуть камешек из вершины v в вершину u, если есть ребро из вершины v в u). Если игрок передвигает камешек из вершины v в вершину u, то «символом» этого раунда называется символ, написанный на ребре из v в u. Есть одно дополнительное правило: ASCII код символа раунда i должен быть не меньше, чем ASCII код символа раунда i - 1 (для i > 1). Раунды нумеруются для всех игроков вместе, иными словами, Макс ходит в нечетных раундах, в Лукас — в четных. Игрок, который не может сделать ход, проигрывает. Камешки могут находиться в одной вершине в одно и то же время.
Поскольку игра занимает некоторое время, а Лукас и Макс должны найти Дарта, у них нет времени для игр. Они спрашивают у вас, кто выиграет, если оба будут играть оптимально?
Вам необходимо определить победителя в игре для всех возможных начальных позиций камешков.
Первая строка содержит два целых числа n и m (2 ≤ n ≤ 100, 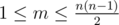 ).
).
Следующие m строк содержат ребра. Каждая строка содержит два целых числа v, u и строчную латинскую букву c (1 ≤ v, u ≤ n, v ≠ u), которые означают, что есть ребро из вершины v в u, и на нем написана буква c. Между каждой парой вершин есть не более одного ребра. Гарантируется, что в графе нет циклов.
Выведите n строк, в каждой по n символов. j-й символ в i-й строке должен быть «A», если Макс побеждает в игре, где ее камешек изначально в вершине i, а камешек Лукаса — в вершине j, и «B» иначе.
4 4
1 2 b
1 3 a
2 4 c
3 4 b
BAAA
ABAA
BBBA
BBBB
5 8
5 3 h
1 2 c
3 1 c
3 2 r
5 1 r
4 3 z
5 4 r
5 2 h
BABBB
BBBBB
AABBB
AAABA
AAAAB
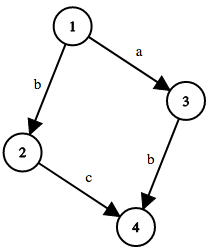
Граф из первого примера показан на рисунке ниже:
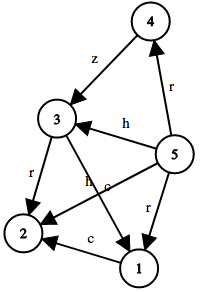
Граф из второго примера показан на рисунке ниже:
| Название |
|---|




