| VK Cup 2018 - Раунд 2 |
|---|
| Закончено |
У Аркадия была прямоугольная таблица из n строк и m столбцов, при этом каждая клетка изначально была покрашена в белый.
Аркадий выполнил несколько (возможно, ноль) операций на ней. На i-й операции он выбрал непустое подмножество строк Ri и непустое подмножество столбцов Ci. Для каждой строки r в Ri и каждого столбца c в Ci он закрасил пересечение строки r и столбца c в черный цвет.
Кроме того, есть дополнительное ограничение: строка или столбец могут выбраны в течение всех операций не более раза. Другими словами, не существует пары (i, j) (i < j) такой, что 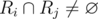 или
или 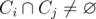 , где
, где  обозначает пересечение множеств, а
обозначает пересечение множеств, а  — пустое множество.
— пустое множество.
Вам дана некоторая таблица. Определите, могла ли она получиться после применения таких операций.
Первая строка содержит два целых числа n и m (1 ≤ n, m ≤ 50) — количество строк и столбцов в таблице, соответственно.
Каждая из следующих n строк содержит строку из m символов, каждый из которых либо «.» (обозначает белую клетку), либо «#» (обозначает черную клетку). Эти строки описывают финальную таблицу.
Если данная таблица может быть получена некоторой корректной последовательностью операций, выведите «Yes»; в противном случае выведите «No» (без кавычек).
Вы можете выводить каждую букву в любом регистре (строчную или заглавную).
5 8
.#.#..#.
.....#..
.#.#..#.
#.#....#
.....#..
Yes
5 5
..#..
..#..
#####
..#..
..#..
No
5 9
........#
#........
..##.#...
.......#.
....#.#.#
No
В первом примере таблицу можно получить за 3 операции, как показано на рисунке ниже.
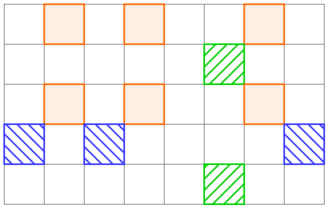
Во втором примере невозможно получить заданную таблицу, так как для того, чтобы закрасить центральную строку, нужно выбрать третью строку и все столбцы в одной операции, но после этого невозможно будет выбрать ни один столбец еще раз, поэтому нельзя будет покрасить оставшиеся клетки в центральном столбце.
| Название |
|---|




