Задано корневое дерево. Определим d(x) как высоту вершины x: высота корня равна 1, высоты любой другой вершины x равна d(y) + 1, где y — предок вершины x.
У данного дерева есть следующее свойство: каждая вершина x с d(x) = i имеет ровно ai детей. Максимальная возможная глубина вершины равна n, an = 0.
Определим fk как количество неупорядоченных пар вершин в дереве таких, что количество ребер на простом пути между ними равно k.
Посчитайте fk по модулю 109 + 7 для всех 1 ≤ k ≤ 2n - 2.
В первой строке записано одно целое число n (2 ≤ n ≤ 5 000) — максимальная глубина вершины.
Во второй строке записаны n - 1 целых чисел a1, a2, ..., an - 1 (2 ≤ ai ≤ 109), где ai — количество детей у каждой вершины x такой, что d(x) = i. Так как an = 0, оно не задается во входных данных.
Выведите 2n - 2 чисел. В k-й строке выведите fk по модулю 109 + 7.
4
2 2 2
14 19 20 20 16 16
3
2 3
8 13 6 9
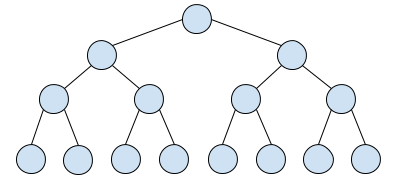
Дерево из первого примера:
| Название |
|---|




