| Codeforces Round 473 (Div. 2) |
|---|
| Закончено |
Махмуд пытался решить задачу вершинного покрытия на дереве. Эта задача формулируется так.
По данному неориентированному дереву, состоящему из n вершин, найдите минимальное число вершин, которые покрывают все рёбра. Формально, нам необходимо найти такой набор вершин, что для каждого ребра (u, v), принадлежащего дереву, или u, или v принадлежит этому набору, или они оба принадлежат ему. Махмуд нашёл следующий алгоритм для решения задачи:
- Возьмём за корень дерева вершину 1.
- Посчитаем количество вершин на чётной глубине и назовём её evenCnt.
- Посчитаем количество вершин на нечётной глубине и назовём её oddCnt.
- Ответом будет являться минимальное из чисел evenCnt и oddCnt.
Глубиной вершины называется число рёбер в кратчайшем пути между этой вершиной и корнем. Глубина корня равна 0.
Эхаб сказал Махмуду, что данный алгоритм неверен, но Махмуд не поверил ему, поскольку он тестировал этот алгоритм на множестве разных деревьев и он всегда выводил правильный ответ. Поэтому Эхаб просит вас помочь найти два таких дерева, состоящих из n вершин, что алгоритм Махмуда выведет неправильный ответ для первого дерева и правильный — для второго.
В единственной строке ввода содержится одно целое число n (2 ≤ n ≤ 105) — число вершин в деревьях, которые необходимо вывести.
Вывод должен состоять из 2 независимых частей, каждая из которых содержит дерево. Алгоритм Махмуда должен получать неправильный ответ для дерева в первой части и правильный — для дерева во второй части. Если по какой-либо причине корректного дерева для какой-то части не существует, выведите -1 только для данной части.
Если ответ для какой-то части существует, он должен содержать n - 1 строку, в каждой из которых должно содержаться 2 целых числа u и v (1 ≤ u, v ≤ n), разделённых пробелами, что будет означать, что между вершинами u и v есть неориентированное ребро. Если выданный вашей программой граф не будет являться деревом или не будет следовать формату выходных данных, ваше решение получит вердикт «Неправильный ответ».
Если существует несколько правильных ответов, выведите любой из них.
2
-1
1 2
8
1 2
1 3
2 4
2 5
3 6
4 7
4 8
1 2
1 3
2 4
2 5
2 6
3 7
6 8
В первом примере существует всего одно дерево с двумя вершинами (вершина 1, соединённая с вершиной 2). Алгоритм всегда получит на нём правильный ответ, поэтому мы вывели - 1 в первой секции, но заметьте, что мы вывели это дерево во второй секции.
Во втором примере:
В первом дереве алгоритм выведет ответ с 4 вершинами, но существует следующий ответ с 3 вершинами: 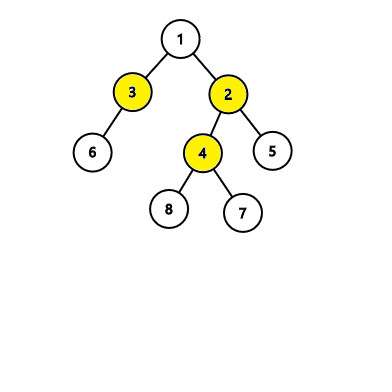 Во втором дереве алгоритм найдёт ответ с 3 вершинами, который верен:
Во втором дереве алгоритм найдёт ответ с 3 вершинами, который верен: 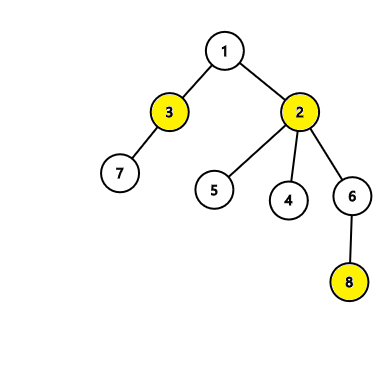
| Название |
|---|




