Вам заданы два массива A и B, размер каждого из которых равен n. Величина ошибки E между этими массивами определятся как 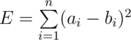 . Вы должны выполнить ровно k1 операций с массивом A и ровно k2 операций с массивом B. За одну операцию вы можете выбрать один элемент массива и увеличить или уменьшить его значение на 1.
. Вы должны выполнить ровно k1 операций с массивом A и ровно k2 операций с массивом B. За одну операцию вы можете выбрать один элемент массива и увеличить или уменьшить его значение на 1.
Выведите минимально возможную величину ошибки после выполнения k1 операций с массивом A и k2 операций с массивом B.
В первой строке находятся три целых числа n (1 ≤ n ≤ 103), k1 и k2 (0 ≤ k1 + k2 ≤ 103, k1 и k2 неотрицательны) — размер массивов и количество операций, которые нужно произвести с массивом A и с массивом B, соотвественно.
Во второй строке заданы n целых чисел a1, a2, ..., an ( - 106 ≤ ai ≤ 106) — массив A.
В третьей строке заданы n целых чисел b1, b2, ..., bn ( - 106 ≤ bi ≤ 106) — массив B.
Выведите единственное число — минимально возможное значение 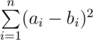 после выполнения ровно k1 операций с массивом A и ровно k2 операций с массивом B.
после выполнения ровно k1 операций с массивом A и ровно k2 операций с массивом B.
2 0 0
1 2
2 3
2
2 1 0
1 2
2 2
0
2 5 7
3 4
14 4
1
В первом тестовом примере, мы не можем применить никаких операций к A или к B. Следовательно, E = (1 - 2)2 + (2 - 3)2 = 2.
Во втором тестовом примере, нам необходимо применить ровно одну операцию к A. Чтобы минимизировать величину ошибки, мы увеличим первый элемент A на 1. Таким образом, A = [2, 2]. Получившаяся величина ошибки E = (2 - 2)2 + (2 - 2)2 = 0. Это минимальная величина ошибки, которую можно получить.
В третьeм тестовом примере, мы можем увеличить первый элемент A до 8, используя все 5 доступных операций. Также первый элемент B можно превратить в 8, используя 6 из 7 доступных операций. Таким образом получаем, A = [8, 4] и B = [8, 4]. Получившаяся величина ошибки равна E = (8 - 8)2 + (4 - 4)2 = 0. Однако, мы должны сделать еще 1 действие над массивом B. Увеличим второй элемент B до 5, получим B = [8, 5] и E = (8 - 8)2 + (4 - 5)2 = 1.
| Название |
|---|




