| Avito Code Challenge 2018 |
|---|
| Закончено |
Рамзес — мастер решения задач про деревья (неориентированные связные графы без циклов)!
Он придумал новую, очень полезную декомпозицию дерева, но, так как обычно он решает задачи только в уме, он не знает, как её найти, и просит вашей помощи!
Его декомпозиция заключается в разбиении ребер дерева на простые пути так, что любая пара путей в декомпозиции будет иметь хотя бы одну общую вершину. Каждое ребро дерева должно войти в ровно один путь.
Помогите Рамзесу, найдите такую декомпозицию данного дерева, или сообщите, что её не существует.
В первой строке дано одно целое число $$$n$$$ ($$$2 \leq n \leq 10^{5}$$$) — количество вершин в дереве.
В каждой из следующих $$$n - 1$$$ строк через пробел записаны два целых числа $$$a_i$$$ и $$$b_i$$$ ($$$1 \leq a_i, b_i \leq n$$$, $$$a_i \neq b_i$$$) — ребра дерева. Гарантируется, что заданные ребра задают дерево.
Если необходимой декомпозиции не существует, в единственной строке выведите «No».
В противном случае в первой строке выведите «Yes», а во второй целое число $$$m$$$ — число путей в декомпозиции.
Следующие $$$m$$$ строк должны содержать по два целых числа $$$u_i$$$, $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$, $$$u_i \neq v_i$$$), разделенных пробелом, обозначающие, что очередной путь декомпозиции — путь между вершинами $$$u_i$$$ и $$$v_i$$$.
Любая пара путей в декомпозиции должна иметь хотя бы одну общую вершину, а каждое ребро дерева должно присутствовать ровно в одном пути. Пути и концы каждого пути можно выводить в любом порядке.
Если существует несколько подходящих декомпозиций, выведите любую.
4
1 2
2 3
3 4
Yes
1
1 4
6
1 2
2 3
3 4
2 5
3 6
No
5
1 2
1 3
1 4
1 5
Yes
4
1 2
1 3
1 4
1 5
Дерево из первого примера изображено на картинке ниже: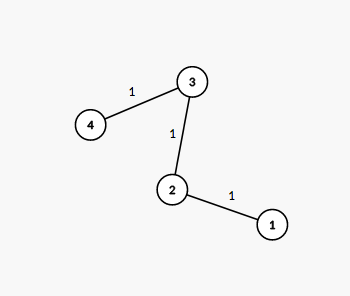 
Рядом с каждым ребром указан номер, к которому принадлежит это ребро в декомпозиции, несложно видеть, что данная декомпозиция удовлетворяет условиям задачи.
Дерево из второго примера изображено на картинке ниже: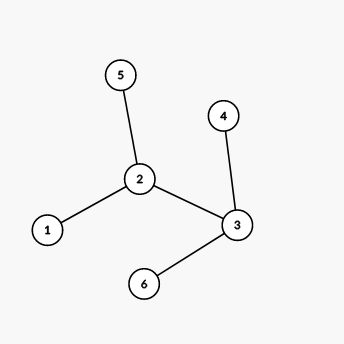 
Можно доказать, что для данного дерева не существует искомой декомпозиции.
Дерево из третьего примера изображено на картинке ниже: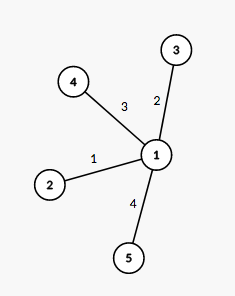 
Рядом с каждым ребром указан номер, к которому принадлежит это ребро в декомпозиции, несложно видеть, что данная декомпозиция удовлетворяет условиям задачи.
