| acmsguru |
|---|
| Finished |
→ Problem tags
No tags yet
No tag edit access
The problem statement has recently been changed. View the changes.
×
480. Gena's Soul Cakes
Time limit per test: 1 second(s)
Memory limit: 65536 kilobytes
Memory limit: 65536 kilobytes
input: standard
output: standard
output: standard
This story is about a boy, called Gena. He is quite a usual boy who goes to school, celebrates All Hallows Eve, also known as Halloween Day, and besides likes programming contests.
One Halloween Day he went from house to house begging for "soul cakes". He happened to collect many "soul cakes" of various tastes that day, and his happiness seemed have no limits. But his elder brother Roma, who was lazy and rude boy, demanded to give him ten cakes. Gena didn't loose control over the situation and gave his brother ten cakes of the same taste in order not to show that he had many tastes, because Roma could demand more cakes. Since that time Gena was thinking about that situation. And after Gena had learnt on Geometry classes about three-dimentional space figures, he invented the following problem.
Consider non-convex figure denoted as "corner" in three-dimentional space. It consists of four equal cubes. One of the cubes has a common face with each of the others. There is the only one point belonging to all four cubes, and this point coinsides one vertex of any cubes (see picture below). Every "corner" is charaterized by two values: color and an integer length of an edge of any cubes (denoted as "size"). "Size" is always equal to some power of two, so only index is given. The problem is to construct a big "corner" comprising given figures under the restiction of using as little number of different colors as possible given "size" of this big "corner".
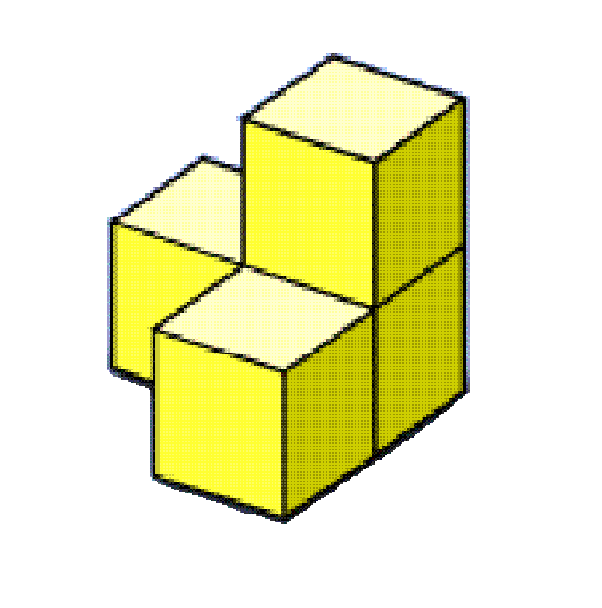
Input
The first line of input contains two space separated integers: c — the number of colors, and k — the index of power of two which is equal to "size" of big "corner" (1 ≤ c, k ≤ 1000). Next c lines contain k integers aij each. aij equals the number of "corners" with color i and "size" 2j. (0 ≤ aij ≤ 1000 for 1 ≤ i ≤ c, 0 ≤ j < k).Output
The first line of output should contain integer n denoting the number of figure types used in constructing big "corner". Next n lines should contain ai, bi, ci denoting color, "size" and number of "corner" of such type respectively. Please, separate these numbers by single spaces. If there are multiple solutions, output any of them. Every type of "corner" should appear in output no more than once. If it is impossible to construct big "corner" even using all figures, print "NO SOLUTION" to output.Example(s)
sample input | sample output |
1 1 8 | 1 1 0 8 |
sample input | sample output |
2 2 1 7 7 0 | 3 1 1 7 1 0 1 2 0 7 |
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/19/2024 05:08:41 (h2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




