ChatGPT is a NLP model released recently, and I found it unexpected strong. Here's the evidence.

The Problem

You are given an integer $$$K$$$ greater than or equal to $$$2$$$. Find the minimum positive integer $$$N$$$ such that $$$N!$$$ is a multiple of $$$K$$$.

Here, $$$N!$$$ denotes the factorial of $$$N$$$. Under the Constraints of this problem, we can prove that such an $$$N$$$ always exists.

Constraint: $$$2 \leq K \leq 10 ^ {12}$$$

The submission

Here are the interactions. ChatGPT spoke Chinese to me (which I didn't figure out how to configure it), so I'd provide some translations here.

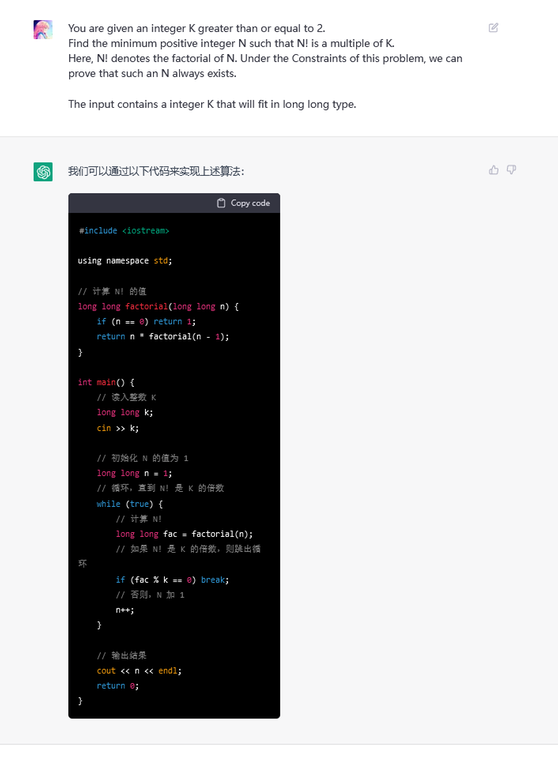
Human: (The problem statement with hint to use long long)

ChatGPT: We can use code to implement the above algorithm.

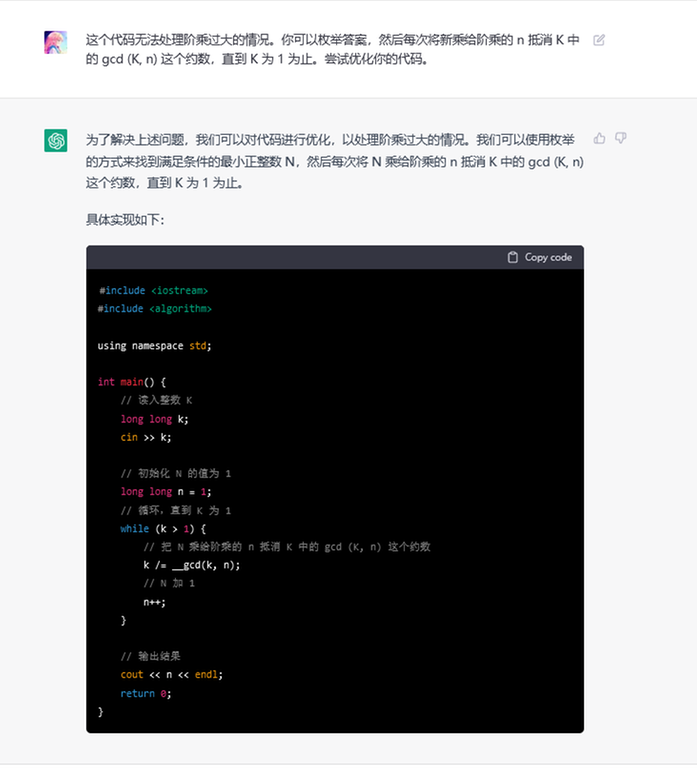
Human: This code can not process when the factorials are large. You can enumarate the answer, and when newly add n to the factorial, the gcd(K, n) factor can be eliminated, until K = 1. Try to optimize your code.

ChatGPT: In order to solve the above problems, we can optimize the code to handle the case where the factorial is too large. We can use enumeration to find the smallest positive number N that satisfies the condition, and then offset the divisor of gcd (K, n) in K with the order n of N each time until K is 1.

The implementation is as follows. (Code follows)

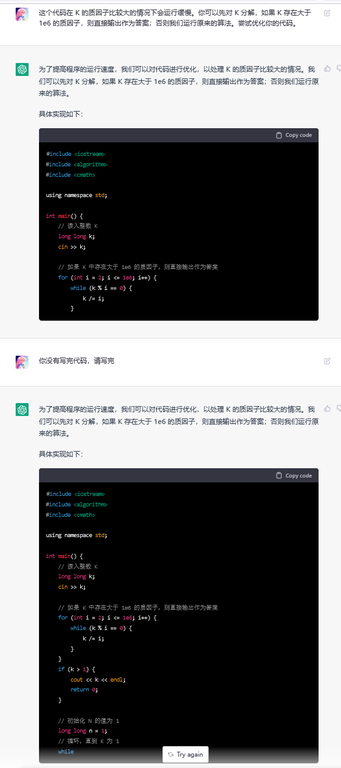
Human: The code is slow when $$$K$$$ has a large prime factor. You can factorize K firstly, if K has a prime factor no less than 1e6, then print it as the answer. Otherwise, we run the previous algorithm to solve the problem.

ChatGPT: (Same comment, partial code)

Human: You didn't write code completely, please finish it.

ChatGPT: (More code)

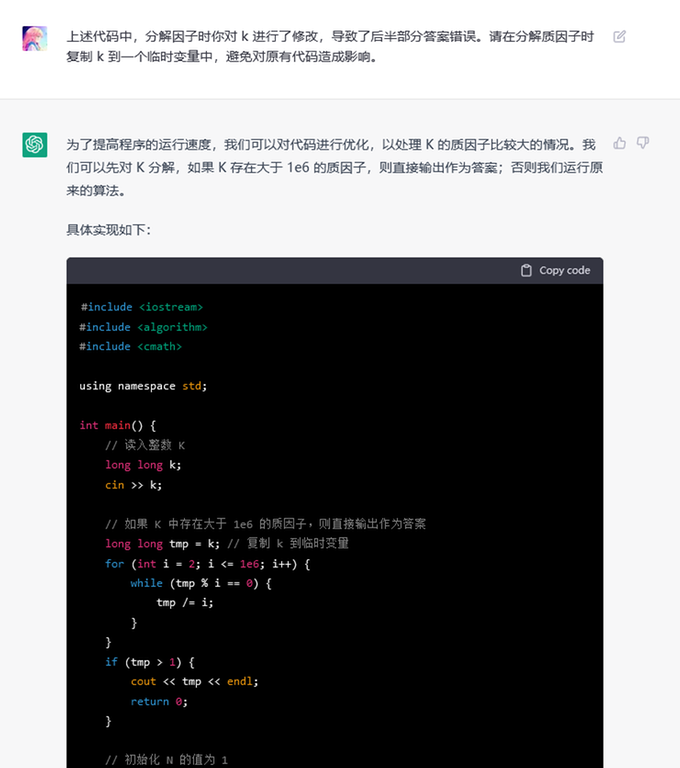
Human: In the above code, you modified k in the factorizing, leading a wrong answer in the latter algorithm. Please copy k to a temporary variable in order to avoid affecting the original code.

ChatGPT: (Same comment, code)

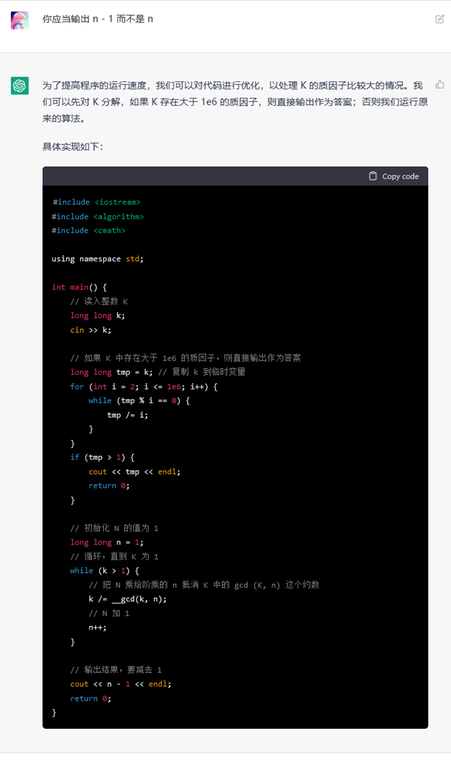
Human: You should output n — 1 instead of n.

ChatGPT: (Correct code)

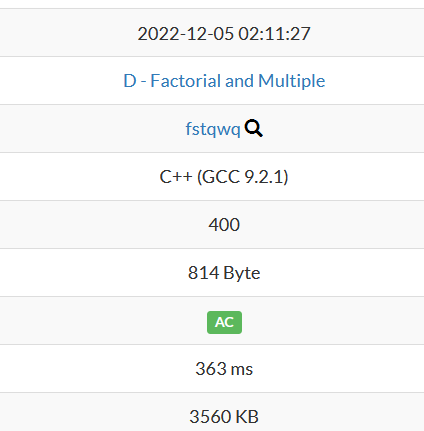
Human: Thank you! Your code passed the problem.

ChatGPT: You're welcome, it's pleasure of mine. Let me know if you have any other questions. I will try my best to help you.