Let's first establish the order we should buy the snacks. Suppose we want to buy a snack of type $$$i$$$ and a snack of type $$$j$$$ ($$$i < j$$$), which one should we buy first? Note that the total value of the snacks dispensed doesn't depend on the order we buy these two snacks. However, if there is only one snack of type $$$i$$$ we cannot buy snack $$$j$$$ first. So we can assume that snacks should be bought in non-descending order (i.e. from left to right).

With this observation, we could solve the problem recursively by trying all the buying strategies. Of course, such a solution will be too slow. To overcome this, we will use dynamic programming to memorize the results. It is quite tricky though, because it requires the following idea: although we buy the snacks from left to right, the buying strategy will be built from right to left.

When planning to buy a type $$$j$$$ snack, we know that we will also get snacks of types $$$1, 2, ..., j-1$$$ (if there are any), though maybe we will get them with a type $$$j$$$ snack, or maybe by buying some other snacks of type less than $$$j$$$. To help us visualise the problem, let's arrange the snacks in a 2D grid: For each snack, stack them to create a column of numbers $$$c_i$$$ of height $$$l_i$$$.

Suppose we choose to buy a type $$$4$$$ and type $$$6$$$ snack. Recall our strategy is to buy snacks from left to right. So firstly, we buy the type $$$4$$$ snack and we get $$$7+2+5$$$ value, then we buy the type $$$6$$$ snack and get $$$2+5+7+2$$$. Note that when we buy the second snack, we do not get a type $$$1$$$ snack, since it has already run out.

However, we can equivalently plan to buy the type $$$6$$$ snack (knowing that whatever other snacks we choose to buy, we will certainly get $$$7+2+5+7+2$$$), and then plan to buy a type $$$4$$$ snack, remembering that we already planned to buy a snack to the right (the type $$$6$$$ snack), so we only get $$$2+5$$$. Note that if we had already planned to buy $$$l_i$$$ or more snacks, then we cannot buy snack $$$i$$$ (since there are none left).

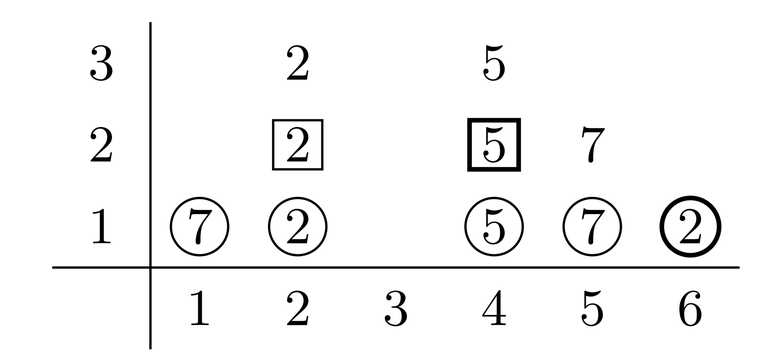
Attributing the snacks this way, we are limited to buying one snack from each row. To make things convenient, let us define $$$t[i, y]$$$ to be the sum of the first $$$i$$$ snacks in the $$$y$$$th row (treating empty cells as $$$0$$$). For example, $$$t[6, 1] = 7 + 2 + 5 + 7 + 2 = 23$$$ and $$$t[4, 2] = 2 + 5 = 7$$$. The table of prefix sums looks like this:

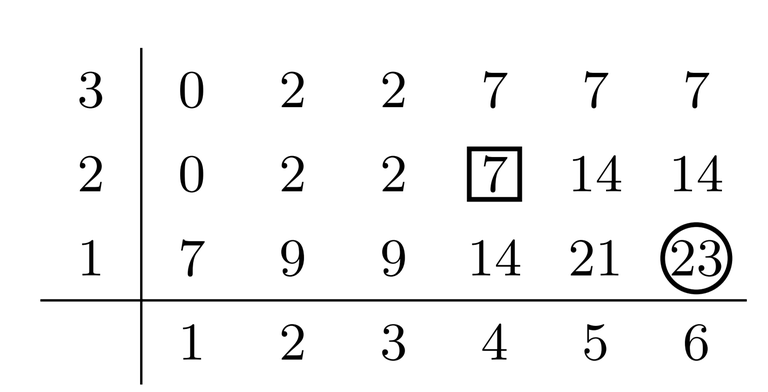
So our problem has been reduced to this: Select a set of squares $$$(i, y)$$$ in the grid such that:

• In each row, the selected square must not be located to the right of the selected square in the previous row.
• In the $$$i$$$th column, we cannot select more than $$$l_i$$$ squares.
• The sum of values $$$c_i$$$ in the selected squares must be at most $$$k$$$ (our budget).
• The sum of $$$t[i, y]$$$ of selected squares is maximised.