Introduction to Disjoint Set Data Strucutres
Hello Codeforces!
I recently read about Disjoint Sets from the book Introduction to Algorithms and wanted to share the learnings in a simplified manner.
So below article(and corresponding videos) is an attempt to create a good starting point for people who:
- want to learn about DSU
- practice some good DSU problems
Contents
- Introduction through an illustrative problem (video version: https://youtu.be/JDycPHW4kIs?si=WEp5Ft2jBWp9KnO2)
- Sample SPOJ Problem and Implementation (video version: https://youtu.be/O4w-aX5mSks?si=vr0XSbyUswcXx-Yv)
- Upcoming Practice Problems
- Some Applications and References
We will learn about disjoint set data structures and their operations union and find through a sample problem.
Illustrative Problem
Q: Given a undirected Graph(V, E), answer Q queries of the form (u, v) where answer to the query is True if there is a path from u to v, false otherwise. 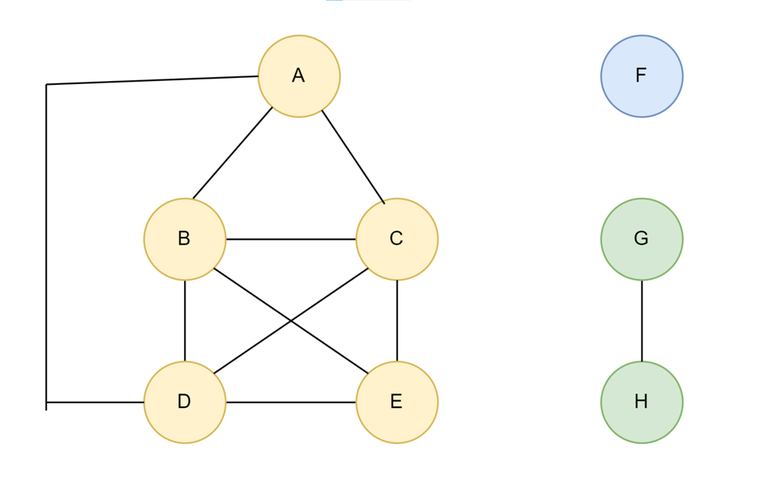
So for above graph:
- query(D,A) = true
- query(D,C) = true
- query(D,F) = false
Some solutions to above problem
Solution1:
- For each query (u, v), perform a BFS/DFS.
- Time Complexity will be O(Q*(V + E))
- In worst case graph can have order of V^2 Edges.
- So worst case complexity can be O(Q*V^2)
Solution2:
- perform 1 BFS/DFS per node of the Graph
- When BFS is done using node X, store all the nodes that can be visited from X.
- Per Query time is O(1) so overall O(Q)
- Preprocessing time is O(V * (V + E)) = O(V^3)
- Hence overall O(Q + V^3)
What is a Disjoint Set Data Structure?
- It is a collection of disjoint dynamic sets. D = {S1, S2, S3, …………, Sk}
- Each set has a Representative R and consists of some elements.
- Assume total elements is N: Size(S1) + Size(S2) + … + Size(Sk) = N
A disjoint set structure supports:
- MAKE-SET(X): Creates a new Set with only element X and representative X.
- FIND(X): Returns the representative of the set to which X belongs.
- UNION(X, Y): Unites the sets containing the elements X and Y into a single new Set. The representative of this set is usually either the representative of Sx or representative of Sy
Diagramatic Example of a disjoint set with total 8 elements and 3 sets:
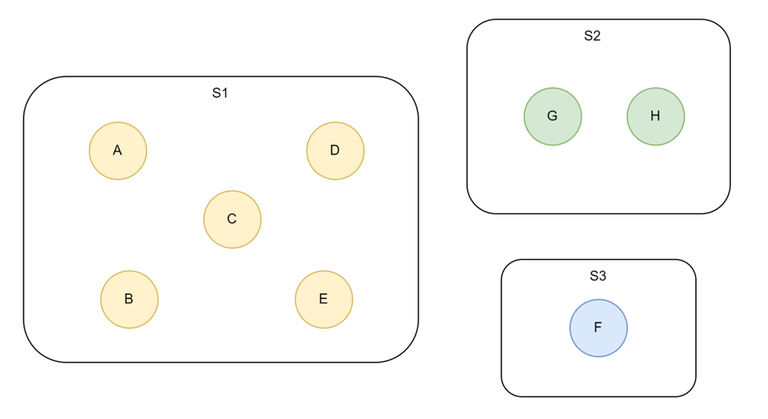
From above:
- Find(H) = G
- Find(F) = F
- Find(B) =Find(E) = A
[Assume that A, G and F are representative elements their sets]
Using Disjoint Set DS for solving the problem
- Run MAKE-SET(u) for each of the V nodes in the graph.
- Run UNION(u,v) for each edge (u,v) in the graph.
- For each Query (u,v): a) If FIND(u) == FIND(v) then answer = true b) Else answer = false
Running 1. and 2. on sample graph constructs the Disjoint set data structure shown in diagram.
Time complexity for DSU solution
Overall Complexity is sum of:
- O(V * MAKE-SET)
- O(E * UNION) = O(V^2 * UNION)
- O(Q * FIND)
Disjoint Set — Linked List Implementation
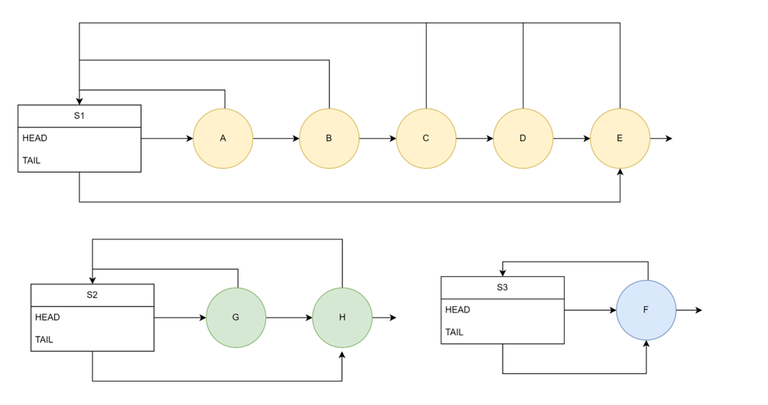
- Each set is represented as a link list.
- The set has HEAD pointer to representative element and also a TAIL pointer.
- Each element of the set has a back-pointer to the set.
Complexity Analysis for link list implementation
- Make Set is O(1) -> only need to create a new set with 1 element
- Find Set is O(1) -> thanks to back pointers
- Union is length of the longer set -> no-thanks to back pointers(all of 2nd set element back-pointers need to be updated to 1st set)
Note: For a total of N elements in the collection there will be at most N-1 union operations as post that all elements will be in the same set.
Worst Case cost of Union is when:
- All sets have size 1.
- 1st union we unite two sets of size 1 and get a set of size 2 -> cost is 1 back pointer change.
- 2nd time we unite a set of size 1 with a set of size 2 -> cost is 2 back pointer change.
- ith time we unite a set of size 1 with a set of size i -> cost is i back pointer change.
- Overall cost over n-1 union operations is 1 + 2 + 3 + .. + n-1 = O(N^2)
Hence union is still O(N) in the worst case.
Weighted Union Heuristic for link list Implementation
While performing union(x,y):
- Always take smaller set and attach it the larger set.
- Need to maintain size of set for each set(which should be easy)
Complexity analysis: Union is now O(logN), but why?
- The cost of a union operation is the cost of changing back pointers of the elements in the smaller set.
- Say we change the back pointer of an Element X belonging to Sx, the resulting set will have at least 2 * Sx elements.(since X belong to smaller set and hence it's backpointer was updated)
- If back pointer of X is changed K times there need to be >= (2^K) * Sx elements
- K can be at most log(N) as we only have N elements.
- hence for a given element we can change the back-pointer at most logN times and overall cost <= NlogN
Revisiting the sample problem
Worst Case complexity of Graph problem has now Improved :)
- O(V * MAKE-SET) = O(V)
- O(E * UNION) = O(V^2 * UNION) = O(V^2 * logV) = O(V^2 * logV)
- O(Q * FIND) = O(Q)
So O(V^2 * logV) instead of O(V^3)
Disjoint Set — Forest Implementation
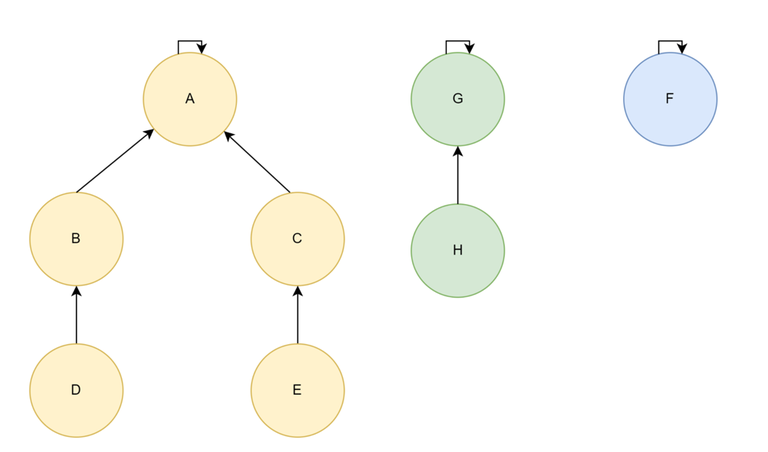
- Each set is represented as a tree.
- Each element is a node of the tree and maintains a pointer to it's parent in the tree.
- The representative element is the parent of itself.
Find(X) = X if parent[X] = X else Find(X) = Find(parent[X])
Forest Implementation — Time Complexities
We may still end up getting a chain :(
Worst case complexities:
- UNION is O(1) * O(FIND) in worst case(only need to change parent pointer of one representative to another, problem is finding the representative using FIND)
- MAKE SET is O(1) in worst case(only need to create a set with 1 element which is it's own parent)
- FIND however is O(N) in the worst case(we may end up getting a link list)
Time Complexities with Heuristics
Heuristic: Union by Rank
While performing union always take the Set(tree) with less height and attach it to the set with greater height.
- Overall height after N-1 union will be order of LogN
- Hence ensuring Find is no worse than LogN
Heuristic: Path Compression When performing find operation, change the parent pointer of each node to the actual representative of the node. 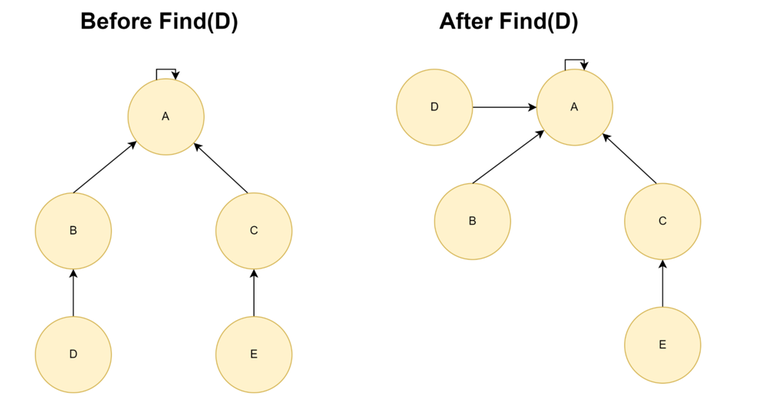
The time complexity when applying both heuristics together is:
- Make Set is O(1)
- Find Set is O(alpha(n))
- Union is amortised O(alpha(n))
What is alpha(n)?
- Where alpha is the inverse of Ackerman function Ak(1)
- Alpha(n) <= 4 for all N <= 16^512
- 16^512 >> 10^80
- 10^80 is the number of atoms in observable universe
Hence for all practical purposes alpha(n) = 4 = constant.
Proof is harder and omitted from scope of this article, refer Introduction To Algorithms by Thomas H. Cormen
Revisiting the sample problem
- Make Set is O(1)
- Find Set is O(1)
- Union is amortised O(alpha(n))
Worst Case complexity of Graph problem has now Improved :)
- O(V * MAKE-SET) = O(V)
- O(E * UNION) = O(V^2 * UNION) = O(V^2 * logV) = O(V^2 * alpha(V))
- O(Q * FIND) = O(Q)
Hence time complexity is now O(V^2 + Q) for all practical purposes.
SPOJ Problem — FRNDCIRC + Generic Implementation
- Problem Link: https://www.spoj.com/problems/FRNDCIRC/
- Solution link: https://youtu.be/O4w-aX5mSks?si=UQJwpjayddjVK5uw
- Code implementation: https://ideone.com/Bdh2It
Upcoming Practice Problems
Currently I have planned the problem https://codeforces.net/problemset/problem/150/B and will be soon adding both a written and video editorial for the same.
Few other practice problems include: https://codeforces.net/blog/entry/55219?#comment-390897 (DSU tag). I will be using some of these to create more editorials.
If you have more suggestions please add in comments.
Applications and References
Some direct applications:
- Finding cycles in a graph
- Kruskals minimum spanning tree algorithm
Some references:
- https://www.youtube.com/@AlgosWithKartik
- Introduction to Algorithms Book
- CP algorithms: https://cp-algorithms.com/data_structures/disjoint_set_union.html





