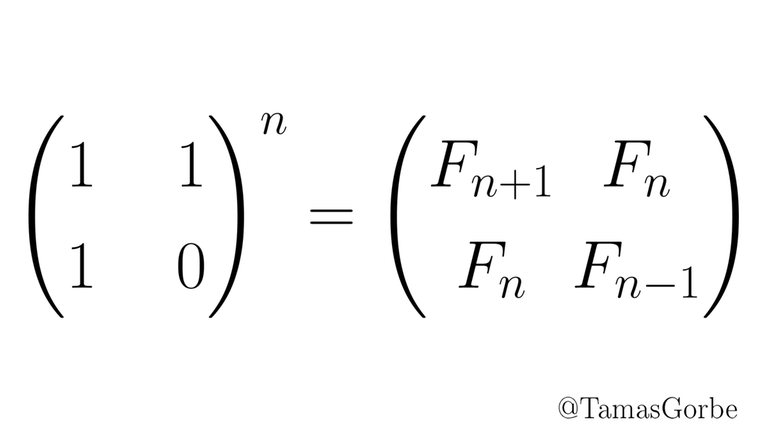Hi ^~^
Part One [Useful Functiones]:
1.1 — power-Function:
[Binary Exponentiation] is a trick which allows to calculate $$$a^n$$$ using $$$O(\log n) $$$
The idea is that we can traverse through all the bits of a number from LSB to MSB in $$$O(\log n) $$$ time.
Write $$$n$$$ in base $$$2$$$.
The number has exactly $$$ \lfloor \log_2 n \rfloor + 1 $$$ digits in base 2, we only need to perform $$$O(\log n) $$$ multiplications, if we know the powers $$$a^1, a^2, a^4, a^8, \dots, a^{2^{\lfloor \log n \rfloor}}$$$ .
1.2 — GCD-Function:
[Euclidean algorithm] is a trick which allows to calculate $$$gcd(a,b) $$$ using $$$O(\log \min(a, b))$$$ The idea is that subtract the smaller number from the larger one until one of the numbers is zero.
For Time Complexity and Binary GCD you can read This.
Note that you can calculate $$$lcm(a,b)$$$ with $$$\frac{a}{gcd(a,b)}\ * b $$$
1.3 — Factorial & nCr & ...:
Sometimes you need to calculate $$$\binom n k $$$
For that first we precompute all factorials modulo $$$ mod $$$ with $$$O(N)$$$.
BUT WE CAN PRECOMPUTE INVERSE OF FAC[I] IN $$$ O(Nlogmod) $$$
1.4 Fibonacci in 20 line:
as you know you can calculate $$$n-th$$$ Fibonacci number with matrix.
it can be proved that :
F[2*n — 1] = F[n]*F[n] + F[n — 1]^2
F[2*n] = (F[n — 1] + F[n + 1])*F[n] = (2*F[n — 1] + F[n])*F[n]
tnx kien_coi_1997 and I_love_tigersugar
1.5 Built-in useful function:
vector<int> a(n);
iota(a.begin(), a.end(), 1);
// a = 123..
random_shuffle(a.begin(), a.end());
// a = random permutation of a
vector<int> ps(n);
partial_sum(a.begin(), a.end(), ps.begin());
// ps[i] = a[0] + a[1] + .... a[i-1] + a[i] ( ps[i] = ps[i-1] + a[i])
vector<int> h(n);
adjacent_difference(a.begin(), a.end(), h.begin());
// h[0] = a[0]
// (i>0) h[i] = = a[i] - a[i-1]
cout << accumulate(a.begin(), a.end(), x) ;
//cout x + a[0] + a[1] + a[2] + ... + a[n]
cout << inner_product(a.begin(), a.end(), b.begin(), 234) << "\n";
// x = 234 + sum(a[i] * b[i])
tnx Igorjan94 for this
Was this blog helpful?