...

...

What is the optimal strategy for Bob?

It is optimal for Bob to negate the $$$x$$$ largest elements of the array. So what should Alice do?

It is optimal for Bob to negate the $$$x$$$ largest elements of the array. So in order to minimize the damage Bob will do, Alice should always remove some number of largest elements.

To solve the problem, we can sort the array and iterate over $$$i$$$ ($$$0 \leq i \leq k$$$) where $$$i$$$ is the number of elements Alice removes. For each $$$i$$$, we know that Alice will remove the $$$i$$$ largest elements of the array and Bob will then negate the $$$x$$$ largest remaining elements. So the sum at the end can be calculated quickly with prefix sums. The time complexity is $$$O(n \log n)$$$ because of sorting.

#include <bits/stdc++.h>
using namespace std; 

void solve(){
    int n, k, x;
    cin >> n >> k >> x;
    
    int A[n + 1] = {};
    for (int i = 1; i <= n; i++)
        cin >> A[i];
    
    sort(A + 1, A + n + 1, greater<int>());

    for (int i = 1; i <= n; i++)
        A[i] += A[i - 1];
    
    int ans = -1e9;
    for (int i = 0; i <= k; i++)
        ans = max(ans, A[n] - 2 * A[min(i + x, n)] + A[i]);
    
    cout<<ans<<"\n";
}

int main(){
    ios_base::sync_with_stdio(0); cin.tie(0); 
    int tc; 
    cin >> tc;
    
    while (tc--) 
        solve();
}

Try to solve the problem for just two integers $$$x$$$ and $$$y$$$. Under what $$$m$$$ are they equal (modulo $$$m$$$)?

How can we use the previous hint and gcd to solve the problem?

For some $$$x$$$ and $$$y$$$, let's try to find all $$$m$$$ such that $$$x \bmod m \equiv y \bmod m$$$. We can rearrange the equation into $$$(x-y) \equiv 0 \pmod m$$$. Thus, if $$$m$$$ is a factor of $$$|x-y|$$$, then $$$x$$$ and $$$y$$$ will be equal modulo $$$m$$$.

Let's solve for some $$$k$$$. A valid partition exists if there exists some $$$m>1$$$ such that the following is true:

• $$$a_1 \equiv a_{1+k} \pmod m$$$
• $$$a_2 \equiv a_{2+k} \pmod m$$$
• ...
• $$$a_{n-k} \equiv a_{n} \pmod m$$$

The first condition $$$a_1 \equiv a_{1+k} \pmod m$$$ is satisfied if $$$m$$$ is a factor of $$$|a_1-a_{1+k}|$$$. The second condition $$$a_2 \equiv a_{2+k} \pmod m$$$ is satisfied if $$$m$$$ is a factor of $$$|a_2-a_{2+k}|$$$. And so on...

Thus, all conditions are satisfied if $$$m$$$ is a factor of:

In other words, all conditions are satisfied if $$$m$$$ is a factor of:

So a valid $$$m$$$ exists for some $$$k$$$ if the aforementioned $$$\gcd$$$ is greater than $$$1$$$.

The time complexity of this will be $$$O(n \cdot \text{max divisors of n})$$$. Note that there should not be a log factor from calculating the gcd given how the gcd will either be halved or stay the same at each point.

#include <bits/stdc++.h>
using namespace std; 

void solve(){
    int n; 
    cin >> n;

    int A[n];
    for (int &i : A)
        cin >> i;
    
    int ans = 0;
    for (int k = 1; k <= n; k++){
        if (n % k == 0){
            int g = 0;
            for (int i = 0; i + k < n; i++)
                g = __gcd(g, abs(A[i + k] - A[i]));
            ans += (g != 1);
        }
    }
    cout<<ans<<"\n";
}

int main(){
    ios_base::sync_with_stdio(0); cin.tie(0); 
    int tc; 
    cin >> tc;

    while (tc--) 
        solve();
}

For some query try to trace your way back to where the $$$k$$$-th number was added.

Here's an example of tracing back:

Suppose the $$$k$$$-th element is the bolded $$$l_2$$$. Finding the $$$k$$$-th element is equivalent to finding the ($$$k \bmod x$$$)-th element.

First, let's precalculate some things:

We can calculate $$$dp$$$ as follows (calculating $$$lst$$$ can be done with similar reasoning):

Now, let's try answering some query $$$k$$$. If we have some $$$dp_i=k$$$ then the answer is $$$lst_i$$$.

Otherwise, let's find the first $$$i$$$ such that $$$dp_i > k$$$. This $$$i$$$ will be a repeat operation and our answer will lie within one of the repetitions. Our list at this point will look like:

Let the $$$k$$$-th element be the bolded $$$l_2$$$ of the final repetition. As you can see, finding the $$$k$$$-the element is equivalent to finding the $$$(k \bmod dp_{i-1})$$$-th element. Thus, we should do $$$k:=k \bmod dp_{i-1}$$$ and repeat! But there is one more case! If $$$k \equiv 0 \pmod {dp_{i-1}}$$$ then the answer is $$$lst_{i-1}$$$.

At this point there are 2 ways we can go about solving this:

#include <bits/stdc++.h>
using namespace std; 

#define ll long long

void solve(){
    int n, q;
    cin >> n >> q;

    ll dp[n + 1] = {};
    int lstAdd[n + 1] = {};
    vector<int> pos;

    for (int i = 1, doAdd = true; i <= n; i++){
        int a, v; 
        cin >> a >> v;

        if (a == 1){
            lstAdd[i] = v;
            dp[i] = dp[i - 1] + 1;
        }
        else{
            lstAdd[i] = lstAdd[i - 1];
            dp[i] = ((v + 1) > 2e18 / dp[i - 1]) ? (ll)2e18 : dp[i - 1] * (v + 1);

            if (doAdd)
                pos.push_back(i);
        }
        // No need to consider any more repetitions after this point
        if (dp[i] == 2e18)
            doAdd = false;
    }
    while (q--){
        ll k; 
        cin >> k;

        for (int i = pos.size() - 1; ~i; i--){
            int idx = pos[i];

            if (dp[idx] > k and dp[idx - 1] < k){
                if (k % dp[idx - 1] == 0){
                    k = dp[idx - 1];
                    break;
                }
                k %= dp[idx - 1];
            }
        }
        cout<<lstAdd[lower_bound(dp + 1, dp + n + 1, k) - dp]<<" \n"[q == 0];
    }
}

int main(){
    ios_base::sync_with_stdio(0); cin.tie(0); 
    int tc; 
    cin >> tc;
    
    while (tc--) 
        solve();
}

#include <bits/stdc++.h>
using namespace std; 

#define ll long long

void solve(){
    int n, q;
    cin >> n >> q;

    ll dp[n + 1] = {};
    int lstAdd[n + 1] = {};

    for (int i = 1; i <= n; i++){
        int a, v; 
        cin >> a >> v;

        if (a == 1){
            lstAdd[i] = v;
            dp[i] = dp[i - 1] + 1;
        }
        else{
            lstAdd[i] = lstAdd[i - 1];
            dp[i] = ((v + 1) > 2e18 / dp[i - 1]) ? (ll)2e18 : dp[i - 1] * (v + 1);
        }
    }
    while (q--){
        ll k; 
        cin >> k;

        while (true){
            int pos = lower_bound(dp + 1, dp + n + 1, k) - dp;
            
            if (dp[pos] == k){
                cout<<lstAdd[pos]<<" \n"[q == 0];
                break;
            }
            if (k % dp[pos - 1] == 0){
                cout<<lstAdd[pos - 1]<<" \n"[q == 0];
                break;
            }
            k %= dp[pos - 1];
        }
    }
}

int main(){
    ios_base::sync_with_stdio(0); cin.tie(0); 
    int tc; 
    cin >> tc;
    
    while (tc--) 
        solve();
}

How do you count the number of good substrings in a string?

We can count the number of good substrings in a string with the counting contribution technique. How can you formulate this into a dp?

$$$\frac{n}{1} + \frac{n}{2} + \cdots + \frac{n}{n} = O(n\log n)$$$

Let's first solve the problem where we are given some string $$$s$$$ and must count the number of good substrings. To do this we use the technique of counting contributions. For every $$$1$$$ in $$$s$$$, we find the number of good substrings containing that $$$1$$$. Consider the following example:

The number of good substrings in this example is $$$a_1 a_2 + a_2 a_3 + a_3 a_4 + a_4 a_5$$$. We can create such array for any string $$$s$$$ and the number of good substrings of $$$s$$$ is the sum of the products of adjacent elements of the array.

This motivates us to reformulate the problem. Instead, we count the number of arrays $$$a_1,a_2,...,a_m$$$ such that every element is positive and the sum of the products of adjacent elements is exactly equal to $$$n$$$. Furthermore, every pair of adjacent elements should have sum minus $$$1$$$ be less than or equal to $$$k$$$. We can solve this with dynamic programming.

The key observation is that we only have to iterate $$$p$$$ up to $$$\lfloor \frac{i}{j} \rfloor$$$ (since if $$$p$$$ is any greater, $$$j \cdot p$$$ will exceed $$$i$$$). At $$$j=1$$$, we will iterate over at most $$$\lfloor \frac{i}{1} \rfloor$$$ values of $$$p$$$. At $$$j=2$$$, we will iterate over at most $$$\lfloor \frac{i}{2} \rfloor$$$ values of $$$p$$$. In total, at each $$$i$$$, we will iterate over at most $$$\lfloor \frac{i}{1} \rfloor + \lfloor \frac{i}{2} \rfloor +\cdots + \lfloor \frac{i}{i} \rfloor \approx i \log i$$$ values of $$$p$$$. Thus, the time complexity of our solution is $$$O(n^2\log n)$$$.

#include <bits/stdc++.h>
using namespace std; 
 
const int md = 1e9 + 7;
 
void solve(){
    int n, k;
    cin >> n >> k;
 
    int dp[n + 1][k + 1] = {};
    int ans = 0;
    
    fill(dp[0] + 1, dp[0] + k + 1, 1);
 
    for (int sum = 1; sum <= n; sum++){
        for (int cur = 1; cur <= k; cur++){
            for (int prv = 1; cur * prv <= sum and cur + prv - 1 <= k; prv++)
                dp[sum][cur] = (dp[sum][cur] + dp[sum - cur * prv][prv]) % md;
 
            if (sum == n)
                ans = (ans + dp[sum][cur]) % md;
        }
    }
    cout<<ans<<"\n";
}
 
int main(){
    ios_base::sync_with_stdio(0); cin.tie(0); 
    int tc; 
    cin >> tc;
 
    while (tc--)
        solve();
}

Use the fact that a good some path $$$p$$$ fully encircles the island if it is impossible to go from an island cell to a cell on the border by only travelling to adjacent or diagonal cells without touching a cell on path $$$p$$$.

Binary search!

For each non-island cell $$$(i, j)$$$, let $$$d_{i,j}$$$ be the minimum Manhattan distance of cell $$$(i, j)$$$ to an underwater volcano. We can find all $$$d_{i,j}$$$ with a multisource BFS from all underwater volcanos. The danger of a round trip is the smallest value of $$$d_{u,v}$$$ over all $$$(u, v)$$$ in the path.

For each query, binary search on the answer $$$k$$$ — we can only visit cell ($$$i, j$$$) if $$$d_{i,j} \geq k$$$. Now, let's mark all cells ($$$i, j$$$) ($$$d_{i,j} \geq k$$$) reachable from ($$$x, y$$$). There exists a valid round trip if it is not possible to go from an island cell to a border cell without touching a marked cell.

The time complexity of this solution is $$$O(nm \log{(n+m)})$$$.

#include <bits/stdc++.h>
using namespace std;

const int mx = 3e5 + 5;
const int diAdj[4] = {-1, 0, 1, 0}, djAdj[4] = {0, -1, 0, 1};
const int diDiag[8] = {0, 0, -1, 1, -1, -1, 1, 1}, djDiag[8] = {-1, 1, 0, 0, -1, 1, 1, -1};

int n, m, q, islandi, islandj; string A[mx]; vector<int> dist[mx]; vector<bool> reachable[mx], islandVis[mx]; queue<pair<int, int>> bfsQ;

bool inGrid(int i, int j){
    return i >= 0 and i < n and j >= 0 and j < m;
}
bool onBorder(int i, int j){
    return i == 0 or i == n - 1 or j == 0 or j == m - 1;
}
void getReach(int i, int j, int minVal){
    if (!inGrid(i, j) or reachable[i][j] or dist[i][j] < minVal or A[i][j] == '#')
        return;
    
    reachable[i][j] = true;

    for (int dir = 0; dir < 4; dir++)
        getReach(i + diAdj[dir], j + djAdj[dir], minVal);
}
bool reachBorder(int i, int j){
    if (!inGrid(i, j) or reachable[i][j] or islandVis[i][j])
        return false;
    
    if (onBorder(i, j))
        return true;
    
    islandVis[i][j] = true;

    bool ok = false;
    for (int dir = 0; dir < 8; dir++)
        ok |= reachBorder(i + diDiag[dir], j + djDiag[dir]);
    return ok;
}
bool existsRoundTrip(int x, int y, int minVal){
    // Reset
    for (int i = 0; i < n; i++){
        reachable[i] = vector<bool>(m, false);
        islandVis[i] = vector<bool>(m, false);
    }
    // Get all valid cells you can reach from (x, y)
    getReach(x, y, minVal);

    // Check if the valid cells you can reach from (x, y) blocks the island from the border
    return !reachBorder(islandi, islandj);
}

int main(){
    ios_base::sync_with_stdio(0); cin.tie(0); 
    cin >> n >> m >> q;

    for (int i = 0; i < n; i++){
        cin >> A[i];
        dist[i] = vector<int>(m, 1e9);

        for (int j = 0; j < m; j++){
            if (A[i][j] == 'v'){
                dist[i][j] = 0;
                bfsQ.push({i, j});
            }
            if (A[i][j] == '#'){
                islandi = i;
                islandj = j;
            }
        }
    }

    // Multisource BFS to find min distance to volcano
    while (bfsQ.size()){
        auto [i, j] = bfsQ.front(); bfsQ.pop();

        for (int dir = 0; dir < 4; dir++){
            int ni = i + diAdj[dir], nj = j + djAdj[dir];

            if (inGrid(ni, nj) and dist[i][j] + 1 < dist[ni][nj]){
                dist[ni][nj] = dist[i][j] + 1;
                bfsQ.push({ni, nj});
            }
        }
    }
    while (q--){
        int x, y;
        cin >> x >> y;
        x--; y--;

        int L = 0, H = n + m;
        while (L < H){
            int M = (L + H + 1) / 2;
            existsRoundTrip(x, y, M) ? L = M : H = M - 1;
        }
        cout<<L<<"\n";
    }
}

If u draw line from island cell extending all the way right, an optimal round trip will cross this line an odd number of times.

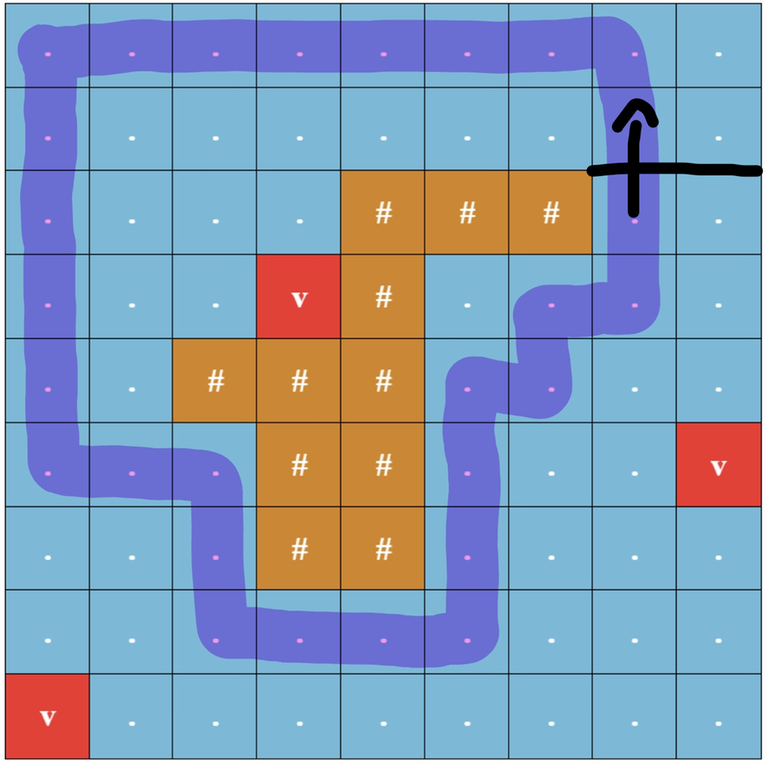
What can your state be? How can we simplify this problem down into finding the path that maximizes the minimum node? How can we solve this classic problem?

For each non-island cell $$$(i, j)$$$, let $$$d_{i,j}$$$ be the minimum Manhattan distance of cell $$$(i, j)$$$ to an underwater volcano. We can find all $$$d_{i,j}$$$ with a multisource BFS from all underwater volcanos. The danger of a round trip is the smallest value of $$$d_{u,v}$$$ over all $$$(u, v)$$$ in the path.

Consider any island cell. Draw an imaginary line along the top border of the cell and extend it all the way to the right of the grid. We can make two observations:

• Any path that starts and ends at the same cell and crosses the line an odd number of times will fully encircle the island and be a round trip.
• An optimal round trip will always cross the line an odd number of times.

Using these observations, we can let our state be $$$(\text{row}, \, \text{column}, \, \text{parity of the number of times we crossed the line})$$$. Naively, we can binary search for our answer and BFS to check if $$$(x, y, 0)$$$ and $$$(x, y, 1)$$$ are connected. This solves the easy version of the problem!

To fully solve this problem, we can add states (and their corresponding edges to already added states) one at a time from highest $$$d$$$ to lowest $$$d$$$. For each query $$$(x, y)$$$, we want to find the first time when $$$(x, y, 0)$$$ and $$$(x, y, 1)$$$ become connected. This is a classic DSU with small to large merging problem. In short, we drop a token labeled with the index of the query at both $$$(x, y, 0)$$$ and $$$(x, y, 1)$$$. Each time we merge, we also merge the sets of tokens small to large and check if merging has caused two tokens of the same label to be in the same component. The time complexity of our solution is $$$O(nm \log nm + q\log^2 q)$$$ with the $$$\log nm$$$ coming from sorting the states or edges. Note that there exists a $$$O(nm \log nm + q\log nm)$$$ solution that uses min path queries on the Kruskal's reconstruction tree or the MST.

#include <bits/stdc++.h>
using namespace std; 
 
const int mx = 3e5 + 5, di[4] = {-1, 0, 1, 0}, dj[4] = {0, -1, 0, 1};
 
int n, m, q, linei, linej, par[mx * 2], ans[mx]; string A[mx]; 
queue<pair<int, int>> bfsQ; vector<int> dist[mx]; vector<array<int, 3>> edges; set<int> S[mx * 2]; 
 
int enc(int i, int j, bool crossParity){
    return i * m + j + crossParity * n * m;
}
bool inGrid(int i, int j){
    return i >= 0 and i < n and j >= 0 and j < m;
}
int get(int i){ 
    return i == par[i] ? i : par[i] = get(par[i]); 
}
void merge(int a, int b, int w){
    a = get(a); b = get(b); 
    
    if (a == b) 
        return;
 
    if (S[a].size() > S[b].size()) 
        swap(S[a], S[b]);
 
    for (int i : S[a]){
        if (S[b].count(i)){
            ans[i] = w; 
            S[b].erase(i);
        }
        else 
            S[b].insert(i);
    }
    par[a] = b;
}
 
int main(){
    ios_base::sync_with_stdio(0); cin.tie(0); 
    cin >> n >> m >> q;
 
    for (int i = 0; i < n; i++){
        cin >> A[i];
        for (int j = 0; j < m; j++){
            dist[i].push_back(1e9);
 
            if (A[i][j] == 'v'){
                dist[i][j] = 0;
                bfsQ.push({i, j});
            }
            if (A[i][j] == '#'){
                linei = i;
                linej = j;
            }
        }
    }
    for (int i = 0; i < q; i++){
        int x, y; cin >> x >> y;
        x--; y--;
        S[enc(x, y, 0)].insert(i);
        S[enc(x, y, 1)].insert(i);
    }
 
    // Multisource BFS to find min distance to volcano
    while (bfsQ.size()){
        auto [i, j] = bfsQ.front(); bfsQ.pop();
 
        for (int dir = 0; dir < 4; dir++){
            int ni = i + di[dir], nj = j + dj[dir];
 
            if (inGrid(ni, nj) and dist[i][j] + 1 < dist[ni][nj]){
                dist[ni][nj] = dist[i][j] + 1;
                bfsQ.push({ni, nj});
            }
        }
    }
 
    // Get the edges
    for (int i = 0; i < n; i++){
        for (int j = 0; j < m; j++){
            // Look at cells to the up and left (so dir = 0 and dir = 1)
            for (int dir = 0; dir < 2; dir++){
                int ni = i + di[dir], nj = j + dj[dir];
 
                if (inGrid(ni, nj) and A[i][j] != '#' and A[ni][nj] != '#'){
                    int w = min(dist[i][j], dist[ni][nj]);
                    
                    // Crosses the line
                    if (i == linei and ni == linei - 1 and j > linej){
                        edges.push_back({w, enc(i, j, 0), enc(ni, nj, 1)});
                        edges.push_back({w, enc(i, j, 1), enc(ni, nj, 0)});
                    }
                    // Doesn't cross the line
                    else{
                        edges.push_back({w, enc(i, j, 0), enc(ni, nj, 0)});
                        edges.push_back({w, enc(i, j, 1), enc(ni, nj, 1)});
                    }
                }
            }
        }
    }
 
    // Sort in reverse and merge to solve offline
    sort(edges.begin(), edges.end(), greater<array<int, 3>>());
 
    // Init DSU stuff
    iota(par, par + mx * 2, 0);
 
    for (auto [w, u, v] : edges)
        merge(u, v, w);
    
    for (int i = 0; i < q; i++)
        cout<<ans[i]<<"\n";
}

#include <bits/stdc++.h>
using namespace std; 
 
const int mx = 3e5 + 5, di[4] = {-1, 0, 1, 0}, dj[4] = {0, -1, 0, 1};
 
int n, m, q, id, linei, linej, par[mx * 4], dep[mx], up[mx * 4][21], minD[mx * 4][21]; 
string A[mx]; queue<pair<int, int>> bfsQ; vector<int> dist[mx], adj[mx * 4]; vector<array<int, 3>> edges; 
 
int enc(int i, int j, bool crossParity){
    // Note that nodes are 1 indexed
    return 1 + i * m + j + crossParity * n * m;
}
bool inGrid(int i, int j){
    return i >= 0 and i < n and j >= 0 and j < m;
}
int get(int i){ 
    return i == par[i] ? i : par[i] = get(par[i]); 
}
void merge(int a, int b, int w){
    a = get(a); b = get(b); 
 
    if (a == b)
        return;
    
    adj[id].push_back(a);
    adj[id].push_back(b);
    minD[id][0] = w;
 
    par[a] = par[b] = id;
    id++;
}
void dfs(int i){
    for (int l = 1; l < 21; l++){
        up[i][l] = up[up[i][l - 1]][l - 1];
        minD[i][l] = min(minD[i][l - 1], minD[up[i][l - 1]][l - 1]);
    }
    for (int to : adj[i]){
        if (to != up[i][0]){
            up[to][0] = i;
            dep[to] = dep[i] + 1;
            dfs(to);
        }
    }
}
int qry(int x, int y){
    int ret = 1e9;
 
    if (dep[x] < dep[y]) 
        swap(x, y);
 
    for (int l = 20, jmp = dep[x] - dep[y]; ~l; l--){
        if (jmp & (1 << l)){
            ret = min(ret, minD[x][l]);
            x = up[x][l];
        }
    }
    if (x == y)
        return min(ret, minD[x][0]);
    
    for (int l = 20; ~l; l--){
        if (up[x][l] != up[y][l]){
            ret = min({ret, minD[x][l], minD[y][l]});
            x = up[x][l]; 
            y = up[y][l];
        }
    }
    return min({ret, minD[x][1], minD[y][1]});
}
 
int main(){
    ios_base::sync_with_stdio(0); cin.tie(0); 
    cin >> n >> m >> q;
 
    for (int i = 0; i < n; i++){
        cin >> A[i];
        for (int j = 0; j < m; j++){
            dist[i].push_back(1e9);
 
            if (A[i][j] == 'v'){
                dist[i][j] = 0;
                bfsQ.push({i, j});
            }
            if (A[i][j] == '#'){
                linei = i;
                linej = j;
            }
        }
    }
 
    // Multisource BFS to find min distance to volcano
    while (bfsQ.size()){
        auto [i, j] = bfsQ.front(); bfsQ.pop();
 
        for (int dir = 0; dir < 4; dir++){
            int ni = i + di[dir], nj = j + dj[dir];
 
            if (inGrid(ni, nj) and dist[i][j] + 1 < dist[ni][nj]){
                dist[ni][nj] = dist[i][j] + 1;
                bfsQ.push({ni, nj});
            }
        }
    }
 
    // Get the edges
    for (int i = 0; i < n; i++){
        for (int j = 0; j < m; j++){
            // Look at cells to the up and left (so dir = 0 and dir = 1)
            for (int dir = 0; dir < 2; dir++){
                int ni = i + di[dir], nj = j + dj[dir];
 
                if (inGrid(ni, nj) and A[i][j] != '#' and A[ni][nj] != '#'){
                    int w = min(dist[i][j], dist[ni][nj]);
                    
                    // Crosses the line
                    if (i == linei and ni == linei - 1 and j > linej){
                        edges.push_back({w, enc(i, j, 0), enc(ni, nj, 1)});
                        edges.push_back({w, enc(i, j, 1), enc(ni, nj, 0)});
                    }
                    // Doesn't cross the line
                    else{
                        edges.push_back({w, enc(i, j, 0), enc(ni, nj, 0)});
                        edges.push_back({w, enc(i, j, 1), enc(ni, nj, 1)});
                    }
                }
            }
        }
    }
 
    // We merge from largest w to smallest
    sort(edges.begin(), edges.end(), greater<array<int, 3>>());
 
    // Init DSU stuff
    id = n * m * 2 + 1;
    iota(par, par + mx * 4, 0);
 
    for (int l = 0; l < 21; l++)
        minD[0][l] = 1e9;
 
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            minD[enc(i, j, 0)][0] = minD[enc(i, j, 1)][0] = dist[i][j];
 
    // Merge
    for (auto [w, u, v] : edges)
        merge(u, v, w);
    
    // DFS to construct the DSU trees
    for (int i = n * m * 4; i; i--)
        if (!up[i][0])
            dfs(i);
    
    // Answer queries via min path queries
    for (int i = 0; i < q; i++){
        int x, y; cin >> x >> y;
        x--; y--;
        cout<<qry(enc(x, y, 0), enc(x, y, 1))<<"\n";
    }
}