I have this problem where I have random points on a 2-D plane and i have to find the circle which is closest to all the Points. I have brute force solution of it which goes like this : 1) Select two sets of two points. 2) Calculate the perpendicular bisector for each pair. 3) Determine the intersection point of these two perpendicular bisectors (one from each set). 4) Verify if the intersection point serves as the center of a circle where the minimum and maximum distances from all points to this center correspond to the points chosen in step 1). 5) If the condition in step 4) holds true, then the intersection point becomes the center of the circle closest to the points, with its radius calculated as half the difference between the maximum and minimum distances plus the minimum distance."
The overall worst case time complexity comes out to be O(n^5). I have found a way to reduce the average case time complexity by utilizing the fact that the outer most 2 point out of the final 4 point that we get will always lie on the Convex hull but the worst case time complexity still remains the same.
Here is the
A sample image where i have random point and with the minimum distance circle. 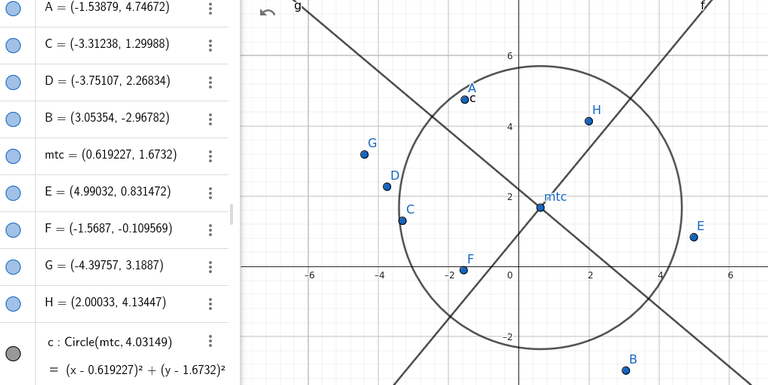 Is there any way that i can reduce the time complexity?
Is there any way that i can reduce the time complexity?






