I haven't seen anyone to write about this technique, so I decided to make a blog about it. I know that it is mostly general intuition, but not everyone really understand it. Also, I would be happy if you add something in comments or correct some errors.
Intuition
I will show intuition of this topic on some easy task, where we will get to the segment tree.
Let's look at some general task, like this: given an array of $$$n$$$ integers, your task is to find the maximum sum of values in a contiguous, nonempty subarray, which is maximum subarray.
This task is very popular, so it has a lot of solutions. We will look at solution using recursion. Assume that maximum subarray cross the middle of it. Using prefix sums and hash-maps, we can find answer is $$$O(n)$$$ or prefix sums with binary search to find answer in $$$O(n\cdot log(n))$$$, it is not important for us. Then assume that it doesn't cross the middle, then we can take maximum subarray on first half of array and second independently by recursion.
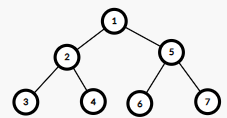
Let's assume, that now we have queries like this: Change number on possition $$$i$$$ to some value $$$x$$$. After each query you need to output maximum subarray of an array. If we brute force this, change element and start old recursion, solution will be to slow. In fact, it is easy to see that too many recursion calls doesn't have this element (it is just apllied to all elements), so there should be a way to optimize it. For example, we can memorize each recursion call. In fact, size of array is never changing, recurion will always be on the same segments. Using this, we can build data structure, which will look like a tree with root at segment [1,n]. Also, each segment [l,r] have two children: [l, $$$ \frac{l+r}{2} $$$ ] and [ $$$\frac{l+r}{2}$$$ +1,r]. Now, if we change element at index $$$i$$$, it will change only nodes, which segments include $$$i$$$ in it. So, we can memorize answer on each node and when we need update element, go from leaf to root of elements which we need, since segments to not intersect. In fact, this is segment tree.
Examples
There are a lot of such examples, which are used just as some another data structures.
For example, merge sort tree. In fact, this is a variation of segment tree, where we just memorize not only answer on the segment or other additional information, but also the array which is on that segment. Why it is called like this? It is because it just memorize all stages of merge sort. So, node [l,r] memorize sorted array [l,r].
Another example is wavelet tree. It is quick sort with the same technique.
Also, trie (preffix tree) is also a good example. It has simple recursion to store, but showes that tree doesn't need to be binary.
Application
339D - Xenia and Bit Operations is a problem which shows this technique. It is literaly in the statement, what we need to memorize.
2002D1 - DFS Checker (Easy Version) is a harder problem, which is not so obvious.



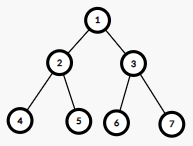 as in the statement to this
as in the statement to this