550A - Две подстроки
Задачу можно решать разными способами. Авторское решение такое: проверим две возможности — когда подстрока "AB" идет первее "BA" и наоборот. Проверять можно следующим образом: найти самое первое вхождение "AB" в исходной строке и рассмотреть подстроки длины 2 правее. Если среди них встретилась подстрока "BA" — ответ "YES". Аналогично проверяется второй случай. Если оба варианта не выполнены, ответ "NO". Сложность решения — O(n), где n — длина исходной строки.
550B - Подготовка олимпиады
Задачу можно решить полным перебором всех подмножеств задач (всего 2n подмножеств). Для каждого из подмножеств проверим, удовлетворяет ли оно условиям задачи. Найдем сумму сложностей всех задач, входящих в подмножество, и убедимся, что она лежит в отрезке [l, r]. Найдем также разность между сложностями максимально сложной задачи и минимально сложной задача подмножества и убедимся, что она не менее x. Если подмножество задач удовлетворяет условиям — увеличиваем общий ответ на 1. Сложность решения задачи — O(2n·n).
550C - Делимость на восемь
Задачу можно решить как минимум двумя способами.
Первый — через "школьный" признак делимости на 8 (число делится на 8 тогда и только тогда, когда число, образованное его последними тремя цифрами, делится на 8). Таким образом, достаточно проверять на делимость на 8 все однозначные, двухзначные и трехзначные числа, образуемые из исходного вычеркиванием цифр. Это можно сделать за O(n3) вложенными циклами по цифрам числа, где n — количество цифр числа.
Второй способ использует динамическое программирование. Будем считать величину dp[i][j], 1 ≤ i ≤ n, 0 ≤ j < 8 — величину, равную 1, если из префикса числа длиной i цифр можно вычеркнуть несколько цифр так, что остаток от деления полученного числа на 8 равен j, и 0 в противном случае. Формулы для пересчета: пусть i-я цифра числа есть ai, тогда dp[i][aimod8] = 1 (по смыслу — однозначные числа), dp[i][(j * 10 + ai)mod8] = max(dp[i][(j * 10 + ai)mod8], dp[i - 1][j]) (по смыслу — дописывание текущей цифры), dp[i][j] = max(dp[i][j], dp[i - 1][j]) (по смыслу — вычеркивание текущей цифры), где 0 ≤ j < 8. Ответ "YES" будет в том случае, когда для некоторого i выполнено dp[i][0] = 1. Для восстановления ответа также нужно завести дополнительный массив prev[i][j], который будет хранить индекс k такой, что при подсчете dp[i][j] пересчет был сделан из dp[i - 1][k]. Сложность такого решения — O(8·n).
550D - Регулярный мост
Докажем, что если k — четное, то решения не существует. Пусть наш граф содержит мост(ы), k = 2s — четное число, степени всех вершин графа равны k. Дерево двусвязных (реберно двусвязных, далее слово "реберных" будет опущено для краткости) компонент исходного графа содержало компоненту, связанную с остальной частью графа только одним мостом (не несколькими мостами!) (на самом деле таких компонент как минимум две, но нам достаточно одной).
Рассмотрим эту компоненту. Удалим мост, связывающий ее с остальной частью графа. Тогда в ней будет всего одна вершина степени k - 1 = 2s - 1 и какое-то количество вершин степени k = 2s. Но тогда она будет содержать только одну вершину нечетной степени, что невозможно.
Построим такой граф для нечетных k. Пусть k = 2s - 1 — нечетное число. Рассмотрим отдельно случай k = 1, тогда, очевидно, подойдет дерево из двух вершин.
Для k ≥ 3 сперва найдем минимальное количество вершин искомого графа. Граф будет содержать как минимум один мост и как минимум две двусвязные компоненты, связанные с остальной частью графа одним мостом. Каждая из этих компонент содержит не менее k + 2 вершин (так как одна вершина связана k - 1 ребрами с другими, остальные имеют степень k = 2s - 1 — нечетное число, т.. количество этих вершин должно быть четным, в то же время оно не может быть меньше k = 2s - 1, то есть оно будет не меньше k + 1, что в сумме с одной вершиной степени k - 1 даст k + 2).
Следовательно, во всем графе будет не менее 2k + 4 вершин. Построим граф с таким количеством вершин.
Занумеруем вершины первой компоненты с 1 до k + 2, вторую компоненту построим аналогично первой. Пусть вершина 1 связана мостом с второй компонентой. Соединим ее k - 1 ребрами с вершинами 2, 3, ..., k. Вершины с номерами 2, 3, ..., k соединим между собой попарно и потом между каждой соседней парой, например 2 - 3, 4 - 5, ... (k - 1) - k, выкинем ребро. После соединим вершины 2, 3, ..., k с вершинами k + 1 и k + 2. Также соединим вершины k + 1 и k + 2 между собой. Тогда все вершины компоненты, кроме первой, будут иметь степень k. Точно так же создаем вторую компоненту и соединяем мостом с первой. Искомый граф построен и содержит O(k) вершин и O(k2) ребер.
Асимптотика решения — O(k2).
550E - Скобки в импликациях
Пусть дано выражение 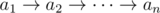 , ai — 0 или 1 для всех i.
, ai — 0 или 1 для всех i.
Покажем, что решения нет только в двух случаях.
1) an = 1.
Это следует из того, что 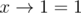 , т. е. никакая расстановка скобок не сможет заменить самую правую 1 выражения на 0.
, т. е. никакая расстановка скобок не сможет заменить самую правую 1 выражения на 0.
2) Выражение имеет вид  или является его суффиксом, содержащим не менее 2 аргументов.
или является его суффиксом, содержащим не менее 2 аргументов.
Это несложно доказать индукцией. Для суффикса  невозможность расстановки скобок очевидна, для более длинных суффиксов любая свертка импликаций либо приведет к тому, что справа появится 1, либо уменьшит число единиц в выражении на 1.
невозможность расстановки скобок очевидна, для более длинных суффиксов любая свертка импликаций либо приведет к тому, что справа появится 1, либо уменьшит число единиц в выражении на 1.
Покажем, что в остальных случаях решение есть.
1) Для выражения 0 ничего делать не надо — ответ 0.
2) Выражение вида 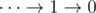 . Можно не расставлять никаких скобок, так как значение такого выражения без скобок равно 0.
. Можно не расставлять никаких скобок, так как значение такого выражения без скобок равно 0.
3) Выражение вида  , где вторая опущенная часть состоит только из единиц. Тогда
, где вторая опущенная часть состоит только из единиц. Тогда  .
.
Асимптотика: O(n).






