Let S(n, k) be a number of states of the game where two bots together can make n moves and first bot can make k moves itself (k ≤ n). It is obvious that S(n, 0) = S(n, n) = n + 1. S(n, k) can be defined by the simple recurrence relation S(n, k) = 1 + S(n - 1, k - 1) + S(n - 1, k). Hence S(n, k) = F(n, k) - 1 where F(n, k) is defined by recurrence relation F(n, k) = F(n - 1, k - 1) + F(n - 1, k). It is a well-known formula for binomial coefficients. So 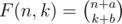where a and b are some constants. They can be found using the foregoing equation for S(n, 0): a = 2, b = 1. Hence 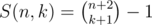. But in the optimal winning strategy both bots make exactly N moves each so n = 2N and k = N. Finally we have that the number of possible states is equal to

.
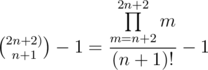