Cutting to the chase

Clearly you don't need a PhD in Computing to sweep in the yard , but one might be usefull in order to know linear and radial sweep algorithm. So , what's all about ? It's just what it sounds it is , sweeping linear ( up to down , for example ) or radial ( making a 360 degrees loop ).

How this can help ? Well...

Linear sweep

Suppose you a set of objects in an Euclidean plane. We need to extract information about some objects. The method of linear sweeping takes a line and moves it on a fixed direction. Usually the line taken would be vertical and the direction would be left to right or up to down.

Quite abstract for the moment , huh ? Let's go to a more specific example.

Rectangle union area

This example is well known. You have a set of rectangles with edges parallel to the OX and OY axes. What is their union area.

Well , first of all , let's take a particular case in order to achieve a different perspective. Let's suppose the lower edges are fixed on the OX axis. This would lead us to the following case :

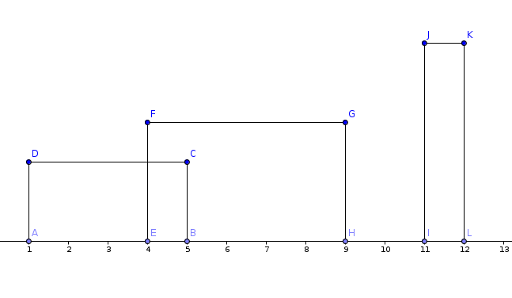
Now let's take a look at the property we established. The property fixes the lower edge. So the only edge we are interested in is the upper edge. The other two will be united by the point projections of the ends of the edge. For example D and C will be projected in B and A. Furthermore , these edges are useless in our problem so we will take into acount only the upper edges.

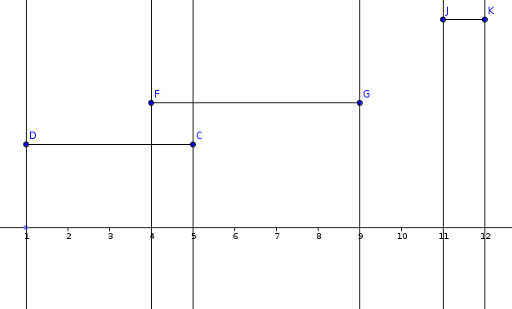
Now as we established that the sweep can go. We will "move" an imaginary line from left to right. As we meet a left corner of the segment we should take it into account for the moment. When we reach it's end it should not be considered any more. On a space between two sweep lines we take all the active segments and memorise the bigest Y. The area added would be maxY * length between sweep lines.

The only remaining question is how we move the imaginary line ? Sorting , of course.

Now let's summarise. We devide each segment in two tipes of querys : in ( a segment is active ) and out ( a segment becomes unactive ). Sort the querys increasingly by X coordinate and for each two consecutive sweep lines take the maximum Y out of the active sweep lines. We can easyly do that with a priority queue. Therefore , the complexity would be O(N log N).

To be sure we understood all , let's look again at the example. The querys will be : in(D) , in(F) , out(C) , out(G) , in(J) , out(K). On interval DF' we have one active segment , therefore maxY = 2. On interval F'C we have two active segments , maxY = 3 from FG segment. On interval CG , maxY = 3 and finally on interval JK , maxY = 5. Total area is 3*2 + 1*3 + 4*3 + 1*5 = 26. Easy.

Radial sweep

Basically , it would go like that: