It's sqrt decomposition. It didn't rime. Bummer...
Cutting to the chase -- better metaphor
“Why not logarithm my problems?” you might ask. My answer will be: you can't always do that.
It has been written about sqrt decomposition many times. Still, many people see as a poor cousin of segment trees or as the crippled child of data structures. There are a lot of tutorials on the topic, but I'll try my best to offer a different perspective and bust the segment tree supremacy by giving this little kid a flamethrower.
???
A story about two eggs
You are given one n-story building and 2 identical eggs. There is a number x, such that any egg dropped from a floor lower than x will survive the fall, while any egg dropped from a floor higher than or equal to x will break.
First of all, let's forget about the fact that we have just 2 eggs. Suppose we have n eggs. Let's denote the verification function of an egg breaking down as f. That's how f works for the following example:
stores | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
----------+---+---+---+---+---+---+---+----
f(store) | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
The egg will break down at 6-th floor. We can observe that f is a non-decreasing function. That means we can binary search on it. So, one might try to break an egg at 4-th floor , then at 6-th floor and finally 5-th floor.
???
For the general case problem look here .
Basics
You are given an array of length n. Answer to m query of types:
- “What is the maximum element in interval [x,y] ? ”.
- The elements on position x take the value y.
The brute force goes like that: we shall iterate from x to y for each query and compute the answer. The update will be O(1) and query O(N). That is O(N*M).
The key element in sqrt decomposition is skipping. Let's define a k-segment as a continuous subsequence from an array that has the length less or equal to k. We shall divide our array in as little k-segments as possible. For example array [1,2,3,4,5,6,7,8,9,10,11,12,13] divided in 3-segments looks like: [1,2,3] [4,5,6] [7,8,9] [10,11,12] [13]. Note that this greedy split of adding elements to a segment if possible ensures us with a maximum number of k-segments.
Now let's apply the k-segment concept to our queries. Let's say we want to find the maximum on interval [3,11]. That is find the maximum out of elements 3] [4,5,6] [7,8,9] [10,11. Let's observe we have “full” and “broken” 3-segments in our example. What is the maximum number of “broken” segments ? It's two ( the left and right border segments ).
Finally , having all this stuff sorted out , I'll present you the final solution.
We record for each segment it's elements and the maximum element. An update is made by replacing the element on the x-th position and updating the maximum on the k-segment. A query can be responded by calculating the maximum on “broken” k-segments and the maximum of the values of the “full” segments.
The complexity is O(K) for an update , O(K+N/K) for a query and O(N) for building the structure. If we take K = sqrt(N) , then the complexity will be O(N+M sqrt N).
Here is an (object oriented) approach to implement the problem above.
You can also read more about the basics (and other stuff) here .
Replacing lazy deletion
You are given an array of length n. Answer to m query of types:
- “What is the maximum element in interval [x,y] ? ”.
- The elements on positions [x,y] take the value z.
The only thing we must keep in addition is a variable ff that works as follows:
- if
ff != 0then the maximum will be fixed - if
ff == 0then we have to compute the maximum
It works just as lazy deletion on segment trees. That is, if we need to look for a value inside a k-segment then is the segment is fixed we update all it's elements with ff. If we need to compute the maximum on a fixed segment is not necessary to go inside it, but rather just respond with value ff. Complexity will be O(N+M sqrt N).
Why the k-segment notation ?
Sometimes taking K=sqrt(N) isn't the best idea. It was the case the following problem form National Olympics in Informatics Romania.
We have a vector v with n elements and a number m. The vector has to be split in exactly m continuous subsequences such that each element has to be in one subsequence. We define the control value of some subsequence as [(maximum-minimum+1)/2]. We have to split the array such that the maximum control value of each subsequence will be as small as possible. ( n <= 1,000,000 and m <= 1000 )
For example if we split the array [13,4,6,19,4,10] in [13,4,6] , [19] , [4,10] we have the control values 5,0,3 so the answer will be 5.
Firstly , let's solve the problem in a not-so-good complexity. We binary search the result, making a greedy verification function. As long as one can expand the current continuous sequence to the right side ( i.e. [(maximum-minimum+1)/2] <= binary_searched_value ) , we move to the right. If we can split the array in m or less sequences, the verification function will return true. The complexity will be O(N log max_ans).
Now we have to improve the complexity of some verification. We split the array in k-sequences ( of length k ). For each sequence keep maximum and minimum. Now, instead of trying to add only one value to the sequence we can try to add k values to it. This will give us the complexity O(N/K+M*K) per verification as we have maximum N/K “full” k-segments to be added and we start to add a new continuous segment to the solution at most M times.
The only thing lest to do it to choose K. If we choose K = sqrt(N) ( <= M ), this will give no improvement. But if we choose K as 100 , this will make our algorithm significantly faster. Final complexity will be O(N + (N/K+M*K) log max_ans).
Give that kid a flamethrower
Now we're talking business, right ?
1. Conex graph
You are given a conex graph with n nodes and m edges. You are given q queries of the type k , a[1] , a[2] … a[k] ( 1 <= a[i] <= m ) and you have to find out for each query if the graph is conex after eliminating edges with indexes a[1] , a[2] … a[k]. Note that each query is independent. ( q*k , m <= 100,000 )
The solution that uses sqrt decomposition splits the queries in groups of k = sqrt(q). Now let's solve the problem for each group of queries.
nbr = int(sqrt(q));
for (int i=1;i<=q;++i)
{
bunch.push_back(i);
if ( int(bunch.size()) == nbr )
{
solve(bunch);
bunch.clear();
}
}
if ( bunch.size() )
solve(bunch);
First of all , let's compress all the nodes that we are not interested in. That is we keep all edges instead of edges in all queries in the current bunch and make a new node for each conex component in this graph. The new graph will have only nodes and no edges.
Let's compute the answer for each query in our bunch. For a query we will add edges in the new graph. Each added edge has a corresponding edge in the old graph. The edges in the old graph that I referred to are all groups of edges for all other k-1 queries.
The complexity will be O(N+sqrt(Q)*K) per bunch. In total the complexity will be O(sqrt(Q) * (N+sqrt(Q)*K)) = O(N*sqrt(Q)+Q*K).
To be sure you understood, let's take a quick example. In the picture the edges marked with red are the first query and the ones with blue are the second one. Suppose we make a bunch out of queries 1 and 2.
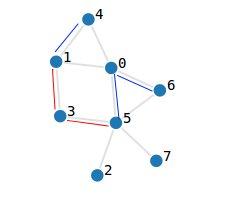
The new graph will be made out of nodes 0' = [0,1,4] , 1' = [3] , 2' = [2,5,6,7]. When we solve query one, edges (1,4) , (0,5) , (0,6) will be added, so in the new graph we will have an edge added between 0' and 2' , therefore the new graph will not be conex. When we solve query two, edges (1,3) , (3,5) are added, so (0',1') and (1',2') are added in the new graph, therefore the new graph will be conex.
You can find a similar problem here .





