I stumbled upon UVA Summing the Lengths of the Longest Increasing Subsequence of Permutations, that basically asks for the first three digits of the sum of the LIS lengths over all permutations of length n. After trying it or a few days, I gave up and searched for information. It is easy to see that:

Where denotes the expected value. It is easy to manage the logarithm of that number with Stirling's approximation, get the fractional part of the logarithm and exponentiate to get the first digits. Nevertheless the core of the problem lies in computing for a random permutation w of length n. I have been reading about the topic, and this paper gives the estimate

Where c ≈  - 1.77108 as a known estimate. Nevertheless, this doesn't give the ouput of uDebug and differs by a  ± 1 margin in about 5% of the cases . I have also asked the question in MathOverflow, and it seems that that estimate is the best known and that there is no polynomial or logarithmic time algorithm for computing .

Finally, I am right now trying to contact the problemsetter baodog looking for clues, as there seems to be few options now:

• He has improved the state of the art in computing without knowing so and expects the contestant to do so too.
• He has not improved the state of the art and expects the contestant to provide a solution.

The last option is ethically questionable. The problem stats page is quite strange too, since the only accepted solution's are Josh Bao's in the 2007 and someone else 20 days later. Also, the old version of the problem asks for the first 5 digits and has a different output for the same input truncating it to the first 3 digits. Moreover, I get the old output by truncating the BDJ estimate to 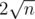as shown by this code. So, can someone provide help to solve this problem and I am not seeing something obvious? Am I right and this problem is impossible with today's knowledge of the matter?