586A - Alena's Schedule

The problem has been prepared by adedalic.

To solve this problem one should remove all leading and trailing zeroes from array and then calculate the number of ones and number of zeroes neighboured by ones. The sum of this values is the answer for the problem.

Complexity: O(n).

586B - Laurenty and Shop

The problem has been prepared by Oleg_Smirnov.

Let's call some path ith if we start it by going i times left, then we cross the prospect and go left n - 1 - i times again. Let d_i be equal to the time we should wait on traffic lights while following i-th path. If we consider any way from the shop to home, it is equal (but reversed) to only path from home to the shop, meaning that we need to find two distinct paths from home to the shop. So the answer to the problem is the sum of the smallest and the second smallest values among d_i. One could easily calculate d_i using calculated d_i - 1, so d_i could be found in one for cycle.

If we will consider only two minimum values among d_i, solution complexity will be O(n).

Complexity: O(n).

585A - Gennady the Dentist

The problem has been prepared by Neon.

Let's store for each child his current confidence value and a boolean indicating whether child had left the queue (or visited the dentist office) or not. Then one could easily process children one by one, considering only children who still are in the queue (using boolean array), and changing stored values.

Such solution has complexity O(n²) and requires author's attention much, especially the case with possible confidence value overflowing. Of course there are much faster solutions not required in our case.

585B - Phillip and Trains

The problem has been prepared by IlyaLos.

One could consider a graph with vertices corresponding to every (x, y) position. I should notice that train positions for each Phillip position are fully restorable from his y coordinate. Edge between vertices u and v means that we could get from position corresponding to u to position corresponding by v in one turn without moving onto a train cell or moving in a cell which will be occupied by some train before the next turn. All we need next is to find whether any finishing position is reachable from the only starting position (using BFS or DFS, or, as soon as graph is a DAG, dynamic programming).

As soon as graph has O(n) vertices and O(n) edges, solution complexity equals to O(n).

585C - Alice, Bob, Oranges and Apples

The problem has been prepared by Edvard.

Firstly, let's understand the process described in problem statement. If one would write a tree of a sum-pairs (x, y) with letters 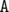and , he would get the Stern–Brocot tree. Let the number of oranges be enumerator and the number of apples be denumerator of fraction. At every step we have two fractions (at first step they are 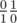) and should replace exactly one of them with their mediant. In such way first fraction is first parent to the left from mediant while second fraction is parent to the right. The process described in statement is, this way, a process of finding a fraction in the Stern-Brocot tree, finishing when the current mediant is equal to current node in the tree and (x, y) pair is the fraction we are searching.

This means that if 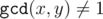, (x, y) does not correspond to any correct fraction and the answer is "Impossible". Other way, we could find it in the tree. If x > y, we should firstly go in the right subtree. Moreover, we could then consider we are searching 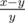from the root. If x < y, we should go left and next consider 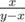from the root. This gives us Euclidian algorithm, which could be realized to work in complexity.

Complexity: O(logn).

585D - Lizard Era: Beginning

The problem has been prepared by danilka.pro.

To solve the problem we will use meet-in-the-middle approach. For we should consider all 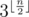variants. Let in some variant approval values of three companions are a, b, c respectively. If we will consider some variant from other half (there are 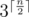of them) and a', b', c' approval values, then to ``merge'' such two parts correctly, two conditions a - b = b' - a' и b - c = c' - b' must be true (a + a' = b + b' = c + c' is true), and the value we are maximizing is a + a'.

This way, to solve the task one could consider every variant from the first half and store for every possible pair (a - b, b - c) the maximum a value achievable (using, for example, the 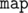structure or any fast sorting algorithm). If one would then consider every variant from the second half, he just need to find (b' - a', c' - b') pair in the structure to get the maximum a value if possible and update answer with a + a' value. Answer restoring is pretty same to the algorithm above.

Such solution has 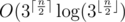complexity.

585E - Present for Vitalik the Philatelist

The problem has been prepared by gridnevvvit.

Let's calculate the number of subsets with gcd equal to 1 — value A. Let's do that using principle of inclusions-exclusions: firstly we say that all subsets is good. The total number of subsets is equal to 2ⁿ. Now let's subtract subsets with gcd divisible by 2. The number of that subsets is equal to 2^cnt₂ - 1 (cnt_i is the number of numbers that is divisable by i). Next we should subtract 2^cnt₃ - 1. Subsets with gcd divisible by 4 we already counted with number two. Next we should subtract 2^cnt₅ - 1. Now we should notice that subsets with gcd divisible by 6 we already processed twice: firstly with number 2, then with — 3, so let's add the number of these subsets 2^cnt₆ - 1. If we continue this process we will get, that for all numbers d we should add the value μ(d)(2^cnt_d - 1), where μ(d) is equals to 0, if d is divisible by square of some prime, 1, if the number of primes in factorization of d is even and  - 1 in other case. So the numbers that is divisible by square of some prime we can ignore, because they have coefficient 0. To calculate values cnt_i we should factorize all numbers and iterate over 2^k divisors with value μ(d) ≠ 0. Now it's easy to see, that the number of subsets with gcd greater than 1 equals to B = 2ⁿ - A. To solve the problem let's fix the stamp that Vitaliy will buy a_i. Let's recalculate the number B for array a without element a_i. To do that we should only subtract those terms that was affected by number a_i. We can do that in 2^k, where k is the number of primes in factorization of the number a_i. It's easy to see that only the subsets with gcd greater than 1, but not divisible by any divisor of a_i, should we counted in answer. To calculate number of those subsets let's again use the principle of inclusions-exclusions. For every divisor d of a_i let's subtract the value 2^cnt_d - 1 from B. So now we got B_i — the number of subsets with gcd greater than 1, but coprime with a_i. The answer to problem is the sum over all B_i. The maximum number of primes in factorization of number not greater than 10⁷ is equal to 8. We can factorize all numbers from 1 to n in linear time by algorithm for finding the smallest divisors for all intergers from 1 to n, or by sieve of Eratosthenes in O(nloglogn) time.

Complexity: O(C + n2^K), where 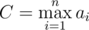, K — is the largest number of primes in factorization of a_i.

585F - Digits of Number Pi

The problem has been prepared by Edvard.

Consider all substrings of string s with length 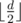. Let's add them all to trie data structure, calculate failure links and build automata by digits. We can do that in linear time using Aho-Korasik algorithm. Now to solve the problem we should calculate dp z_{i, v, b1, b2, b}. State of dp is described by five numbers: i — number of digits, that we already put to our number, v — in which vertex of trie we are, b₁ — equals to one if the prefix that we built is equals to prefix of x, b₂ — equals to one if the prefix that we built is equals to prefix of y, b — equals to one if we already have some substring with length 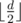on the prexif that we built. The value of dp is the number of ways to built prefix with the given set of properties. To update dp we should iterate over the digit that we want to add to prefix, check that we still is in segment [x, y], go from vertex v to the next vertex in automata. So the answer is the sum by all v, b₁, b₂ z_{b, v, v1, v2, 1}.

Complexity: O(nd²).