595A — Виталий и ночь

Простая задача на реализацию. Проитерируемся по i от 1 до n, а внутри проитерируемся по j от 1 до m, причем на каждой итерации будем увеличивать j на два. Если на текущей итерации a[i][j] = '1' или a[i][j + 1] = '1' увеличим ответ на один.

Асимптотика решения — O(nm).

595B — Паша и телефон

Будем считать ответ для каждого блока отдельно и умножать ответ для предыдущих блоков на ответ для текущего блока, при этом не забывая брать результат перемножения по модулю.

Для блока длины k ответ считается следующим образом. Пусть для этого блока число должно делиться на x и не должно начинаться с цифры y. Тогда ответ для этого блока — количество чисел из k цифр, делящихся на x, минус количество чисел, начинающихся с цифры y и состоящих из k цифр, плюс количество чисел, начинающихся с цифры y - 1 (только если y > 0) и состоящих из k цифр.

Асимптотика решения — O(n / k).

594B — Максим и велосипед

Главное утверждение для решения этой задачи — в середине дистанции каждого соревнования датчик должен находиться либо в самой верхней точке колеса, либо в самой нижней точке колеса.

Для того, чтобы посчитать ответ, воспользуемся бинпоиском. Если центр колеса прошел расстояние c то датчик переместился на расстояние c + rsin(c / r), если в середине датчик находился сверху колеса, или на расстояние c - rsin(c / r), если в середине датчие находился снизу колеса, где r — это радиус колеса.

Асимптотика решения — .

594С — Эдо и магниты

Найдем центры прямоугольников и умножим их координаты на два, чтобы далее работать с целыми координатами. Тогда подходящим холодильником (для всех точек) является прямоугольник, содержащий все точки, но с длинами сторон, округленными вверх к ближайшему четному числу.

Представим теперь, что удаляем магниты с холодильника последовательно, постепенно "уменьшая" прямоугольник. Очевидно, что каждый раз выгодно удалять только те точки, что лежат на какой-то из четырех сторон прямоугольника. Переберем 4^k вариантов того, как мы будем это делать, с помощью рекурсии, каждый раз удаляя одну из еще не удаленных точек с максимальным или минимальным значением по одной из координат. Если мы будем поддерживать 4 массива (или два массива в виде дека), то это можно делать за O(1) амортизированно. Такое решение будет работать за O(4^k).

Можно также заметить, что описанный выше алгоритм удаляет всегда несколько самых правых, левых, верхних, и нижних точек. Можно перебрать, как k распределится среди этих величин и промоделировать удаление с помощью, например, описанных выше 4 массивов. Такое решение имеет асимптотику O(k⁴).

594D — REQ

Для подсчета ответа на каждый запрос будем пользоваться формулой 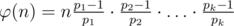, где p₁, p₂, ..., p_k — все простые, делящие n. Эту формулу каждый может попробовать доказать или воспользоваться уже существующими доказательствами. Все вычисления ниже производим по модулю 10⁹ + 7

Предположим теперь, что мы решаем задачу для фиксированного левого конца отрезка l, отбросив все элементы левее. Любой запрос теперь превращается в запрос на префиксе массива. Тогда, судя по формуле, для каждого простого p нас интересует лишь его самое левое вхождение, потому что все остальные вхождения не будут влиять на правую часть в приведенной выше формуле. Превратим наш запрос на значение функции Эйлера в запрос произведения на префиксе: сначала проинициализируем 23:13:15 дерево Фенвика произведений единицами, затем сделаем умножения в точках l, l + 1, ..., n значениями соответствующих элементов a_l, a_l + 1, ..., a_n, затем для каждого самого левого вхождения простого p в позицию i сделаем умножение в точке i на значение 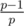. Нетрудно убедиться, что теперь запрос на префиксе определенной длины даст правильный ответ для отрезка той же длины с левым концом в l. Такую подготовку для фиксированного левого конца можно осуществить за 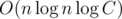, где C — максимальное значение элемента (этот логарифм соответствует количеству простых в разложении какого-то из a_i).

Нас интересуют все левые концы, поэтому научимся переходить от одного из них к другому. В самом деле, пусть все было посчитано для левого конца l и мы хотим теперь перейти к левому концу l + 1. Нас перестает интересовать a_l внутри левой части формулы, поэтому сделаем умножение в дереве Фенвика в точке l на значение a_l^- 1. Так же нас перестают интересовать все простые внутри a_l (а они, очевидно, самые левые среди своих вхождений), поэтому сделаем так же умножения в точке l на все значения 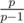. Однако у каждого из этих простых могли существовать другие вхождения, которые теперь станут самыми левыми. Добавим их с помощью умножений, описанных выше. С помощью сортировок (или векторов) переход между соседними левыми концами реализуется за суммарную .

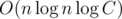Чтобы правильно отвечать на запросы, их так же нужно правильно отсортировать (или поместить в динамический массив), и ответ на запрос будет совершать операций. Суммарная асимптотика всего решения 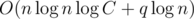операций и 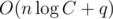дополнительной памяти.

594E — Разрезание строки

Опишем жадный алгоритм, который позволяет решить задачу при k > 2 для любой строки S.

Будем считать, что мы всегда переворачиваем некоторый префикс строки S (возможно, длины 1, подробнее ниже). Поскольку мы стремимся минимизировать строку лексикографически, легко убедиться в том, что мы будем переворачивать такие и только такие префиксы, префикс которых (после переворачивания) совпадает с минимальным лексикографически суффиксом перевернутой строки S (обозначим ее S^r), в частности, это префикс, совпадающий по длине с минимальным суффиксом S^r (операция переворачивания префикса S равносильна замене его суффиксом S^r соответствующей длины).

Обозначим минимальный лексикографически суффикс строки S^r как s. Можно показать, что никакие два вхождения s в S^r не пересекаются, так как в противном случае строка s была бы периодической, и минимальный суффикс имел бы меньшую длину. Значит, строка S^r имеет вид t_ps^a_pt_p - 1s^a_p - 1t_p - 2... t₁s^a₁, где s^x означает конкатенацию строки s x раз, a₁, a₂, ..., a_p — натуральные числа, а строки t₁, t₂, ..., t_p — некоторые непустые (кроме, возможно, t_p) строки, не содержащие s в качестве подстроки.

Перевернув некоторый подходящий префикс строки S, мы перейдем к меньшей строке S', при этом минимальный суффикс s' этой перевернутой строки S'^r не может быть лексикографически меньше, чем s (это каждый может доказать самостоятельно), поэтому мы стремимся сделать так, чтобы s' осталось равным s, что позволит увеличить префикс вида s^b в ответе (а значит и минимизировать его). Легко доказать, что максимальное b, которое мы можем получить, равно a₁ в случае p = 1 и 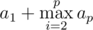(в случае, если p \geq 2$). Действительно, после таких операций префикс ответа будет выглядеть как s^a₁s^a_it_is^a_i - 1... s^a₂t₂. Поскольку t_{i} — непустые строки, увеличить количество конкатенаций s в префиксе ответа никак не получится. Заметим, что переворот второго префикса (s^a_i...) возможен, так как k > 2.

Из описанных выше утверждений следует, что при k > 2 для оставшейся строки всегда следует переворачивать префикс, который после переворота совпадает с суффиксом строки S^r вида s^a₁. Чтобы находить этот суффикс каждый раз, достаточно один раз построить декомпозицию Линдона (с помощью алгоритма Дюваля) перевернутой исходной строки и аккуратно объединять равные строки в ней. Единственным случаем остается вариант, когда префикс оставшейся строки переворачивать не нужно — его можно обработать как конкатенацию последовательных переворачиваемых префиксов длины 1.

Поскольку для k = 1 задача тривиальна, осталось решать задачу для k = 2, то есть деление строки на две части (префикс и суффикс) и какой-то способ их переворачивания. Случай, когда ничего не переворачивается, нам не интересен, рассмотрим два других случая:

1. Префикс не переворачивается. В таком случае обязательно переворачивается суффикс. Два варианта строки с перевернутым суффиксом можно сравнивать за O(1) с помощью z-функции строки S^r#S.

2. Префикс переворачивается. Для решения этого случая можно воспользоваться утверждениями из разбора задачи F Яндекс.Алгоритма 2015 из Раунда 2.2 авторства GlebsHP и рассмотреть только два варианта поворота префикса, перебрав для каждого из них все два варианта поворота суффикса.

Остается выбрать из двух случаев лучший ответ. Итоговая асимптотика решения O(|s|).