This is a technical problem. You should do exactly what is written in problem statement.
600B - Queries about less or equal elements
Let's sort all numbers in a. Now let's iterate over elements of b and for element bj find the index of lowest number that is greater than bj. We can do that using binary search. That index will be the answer for value bj.
Complexity: O(nlogn).
Let's denote cntc — the number of occurences of symbol c. Let's consider odd values cntc. Palindrome can not contain more than one symbol c with odd cntc. Let's denote symbols with odd cntc as a1, a2...ak (in alphabetical order). Let's replace any one of symbols ak with symbol a1, ak - 1 with a2 and so on until the middle of a. Now we have no more than one odd symbol. If we have some let's place it in the middle of the answer. First half of answer will contain 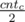 occurences of symbol c in alphabetical order. The second half will contain the same symbols in reverse order. For example for string s = aabcd at first we will replace d by
occurences of symbol c in alphabetical order. The second half will contain the same symbols in reverse order. For example for string s = aabcd at first we will replace d by
Unable to parse markup [type=CF_TEX]
in the middle and after permuting the symbols we got abcba. Easy to see that it's the optimal solution.Compexity: O(n).
600D - Area of Two Circles' Intersection
If the circles don't intersect than the answer is 0. We can check that case with only integer calculations (simply by comparing the square of distance between centers with square of the sum of radiuses). If one of the circles is fully in other then the answer is the square of the smaller one. We can check this case also with only integer calculations (simply by comparing the square of distance between centers with square of the difference of radiuses).
So now let's consider the general case. The answer will be equal to the sum of two circular segments. Let's consider the triangle with apexes in centers if circles and in some intersecting point of the circles. In that triangle we know all three sides so we can compute the angle of the circular segment. So we can compute the square of circular sector. And the only thing that we should do now is to subtract the square of triangle with apexes in the center of circle and in the intersecting points of circles. We can do that by computing the half of absolute value of cross product. So we have the following formulas:
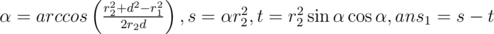 ,
,
where d is the distance between centers of the circles. And also we should do the same thing with second circle by replacing of indices 1 ≤ ftrightarrow2.
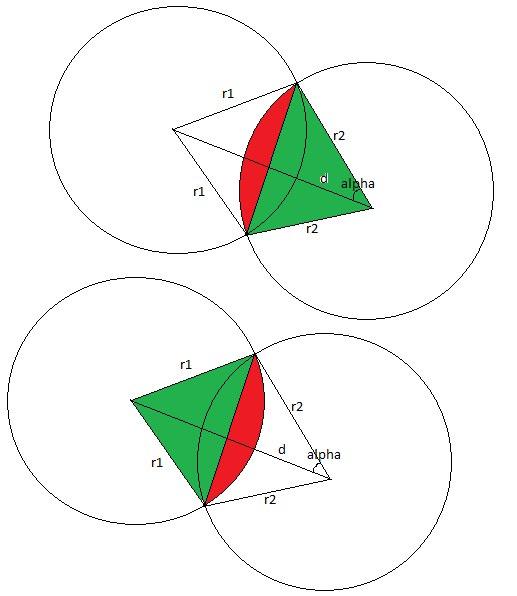
Complexity: O(1).







