Consider a well-known problem: given a static array of size n, answer m queries of kind "how many numbers on [l, r] have value less than x". The standard solution is to build a segment tree where in every node we store a sorted vector. To answer a query we do a binary search in every corresponding node, achieving 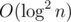per query time complexity.

There is a method to reduce time complexity to 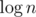per query, called partial cascading. Instead of doing binary search in each node we do it only in the root, and then "push" its result to children in O(1).

For years I thought that the second approach is blazingly faster than the first one. And today I've made a test. I implemented both approaches in a pretty straightforward way and tested them on a random data. The results were quite surprising.

Partial cascading: 760 ms

Top-down implementation: 670 ms

Bottom-up implementation: 520 ms

The first one is , others are 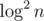! Time is averaged over several consecutive runs. Test data is generated randomly with n = 100000, m = 200000.

Why doesn't partial cascading give any improvements? Am I implementing it in an improper way? Anyway, this might be worth taking a look.