This round was unusual: some of problems was prepared by students and employees of Saratov State U for some of past olympiads and one of problems was prepared by dalex for Codeforces regular round but was not used there.
Let's sort the array in nonincreasing order. Now the answer is some of the first flash-drives. Let's iterate over array from left to right until the moment when we will have the sum at least m. The number of elements we took is the answer to the problem.
Complexity: O(nlogn).
Let's denote cnti — the number of books of i th genre. The answer to problem is equals to 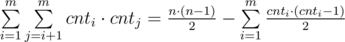 . In first sum we are calculating the number of good pairs, while in second we are subtracting the number of bad pairs from the number of all pairs.
. In first sum we are calculating the number of good pairs, while in second we are subtracting the number of bad pairs from the number of all pairs.
Complexity: O(n + m2) or O(n + m).
Denote s — the sum of elements in array. If s is divisible by n then the balanced array consists of n elements  . In this case the difference between maximal and minimal elements is 0. Easy to see that in any other case the answer is greater than 0. On the other hand the array consists of
. In this case the difference between maximal and minimal elements is 0. Easy to see that in any other case the answer is greater than 0. On the other hand the array consists of 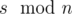 numbers
numbers 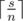 and
and 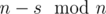 numbers
numbers 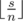 is balanced with the difference equals to 1. Let's denote this balanced array b. To get array b let's sort array a in nonincreasing order and match element ai to element bi. Now we should increase some elements and decrease others. In one operation we can increase some element and decrease another, so the answer is
is balanced with the difference equals to 1. Let's denote this balanced array b. To get array b let's sort array a in nonincreasing order and match element ai to element bi. Now we should increase some elements and decrease others. In one operation we can increase some element and decrease another, so the answer is 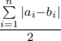 .
.
Complexity: O(nlogn).
609D - Gadgets for dollars and pounds
If Nura can buy k gadgets in x days then she can do that in x + 1 days. So the function of answer is monotonic. So we can find the minimal day with binary search. Denote lf = 0 — the left bound of binary search and rg = n + 1 — the right one. We will maintain the invariant that in left bound we can't buy k gadgets and in right bound we can do that. Denote function f(d) equals to 1 if we can buy k gadgets in d days and 0 otherwise. As usual in binary search we will choose 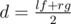 . If f(d) = 1 then we should move the right bound rg = d and the left bound lf = d in other case. If binary search found the value lf = n + 1 then the answer is - 1, otherwise the answer is lf. Before binary search we can create two arrays of gadgets which are selling for dollars and pounds, and sort them. Easy to see that we should buy gadgets for dollars on day i ≤ d when dollar costs as small as possible and j ≤ d when pounds costs as small as possible. Let now we want to buy x gadgets for dollars and k - x gadgets for pounds. Of course we will buy the least cheap of them (we already sort the arrays for that). Let's iterate over x from 0 to k and maintain the sum of gadgets for dollars s1 and the sum of gadgets for pounds s2. For x = 0 we can calculate the sums in O(k). For other x's we can recalculate the sums in O(1) time from the sums for x - 1 by adding gadget for dollars and removing gadget for pounds.
. If f(d) = 1 then we should move the right bound rg = d and the left bound lf = d in other case. If binary search found the value lf = n + 1 then the answer is - 1, otherwise the answer is lf. Before binary search we can create two arrays of gadgets which are selling for dollars and pounds, and sort them. Easy to see that we should buy gadgets for dollars on day i ≤ d when dollar costs as small as possible and j ≤ d when pounds costs as small as possible. Let now we want to buy x gadgets for dollars and k - x gadgets for pounds. Of course we will buy the least cheap of them (we already sort the arrays for that). Let's iterate over x from 0 to k and maintain the sum of gadgets for dollars s1 and the sum of gadgets for pounds s2. For x = 0 we can calculate the sums in O(k). For other x's we can recalculate the sums in O(1) time from the sums for x - 1 by adding gadget for dollars and removing gadget for pounds.
Complexity: O(klogn).
609E - Minimum spanning tree for each edge
TODO
TODO







