628A - Теннисный турнир
Задача предложена пользователем unprost.
В этой задаче можно было просто промоделировать процесс. А можно было заметить, что после каждого матча один игрок выбывает. Всего выбывших n - 1. Таким образом, всего нам нужно (n - 1) * (2b + 1) бутылок воды. Полотенец, конечно, нам нужно np штук.
Сложность: O(log2n), O(logn) или O(1) в зависимости от реализации.
628B - Новый скейтборд
Эта одна из задач предложенных пользователями Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A.
Ключевым для решения задачи является наблюдение, что число делится на 4 тогда и только тогда, когда его последние две цифры делятся на 4. Таким образом, для подсчёта ответа достаточно сначала посчитать количество подстрок длины один. Далее нужно рассмотреть пары соседних цифр таких, что они образуют двузначное число кратное 4-м и прибавить к ответу индекс правого из них.
Сложность: O(n).
628C - Медведь и расстояние между строками
Задачи предложена и подготовлена Камилем Дебовски Errichto.
В этой задаче можно действовать жадно. Будем идти по строке слева направо. Рассмотрим наибольшее расстояние d, которое мы можем получить на этой позиции (это либо расстояние вниз до буквы 'a', либо вверх до буквы 'z'). Пусть v = min(d, k). Поставим на текущей позиции букву на расстоянии v (вниз или вверх), а значение k уменьшим на v. Если после обработки всей строки, k оказалось больше нуля, то ответа не существует. В противном случае мы нашли ответ.
Сложность: O(n).
628D - Волшебные числа
Более простую версию задачи предложил Kareem Mohamed Kareem_Mohamed.
Обозначим ответ на задачу как f(a, b). Заметим, что f(a, b) = f(0, b) - f(0, a - 1) или что то же самое f(a, b) = f(0, b) - f(0, a) + g(a), где g(a) равно единице если a является волшебным число, иначе g(a) равно нулю. Далее будем решать задачу для отрезка [0, n].
Далее приводится стандартная техника, которую иногда называют 'динамикой по цифрам'. Её можно реализовать двумя способами, в первом перебирается длина префикса числа, который совпадёт с префиксом числа n. Следующий символ может быть произвольным меньшим соответствующей цифры в n, а далее любые цифры. Но я расскажу о втором подходе.
Пусть zijk равно количеству волшебных префиксов длины i, дающих остаток j при делении на m. При этом если k = 0, то префикс должен быть строго меньше префикса числа n, а если k = 1, то префикс должен быть равен префиксу числа n (больше он быть не может). Будем делать динамику вперёд. Переберём цифру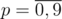 
, которую мы поставим на позиции i. При этом нам нужно проверить, что если позиция чётна то эта цифра должна быть равна d, а в противном случае она не может быть равна d. Также нужно проверить, что если k = 1, то эта цифра не может быть больше соответствующей цифры в числе n. Теперь поймём в какое состояние мы попадём после такого перехода. Конечно, i' = i + 1. Согласно схеме Горнера j' = (10j + p) mod m. Легко видеть, что 
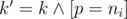. Для перехода нужно сделать zi'j'k' + = zijk. Конечно, нужно не забыть делать все операции по модулю 109 + 7.
Сложность: O(nm).
628E - Zbazi в Zeydabad
Задача предложена Ali Ahmadi Kuzey.
Давайте сначала сделаем предподсчёт zlij, zrij, zldij — наибольшее количество букв 'z' влево, вправо и влево-вниз от позиции (i, j). Это легко сделать за O(nm). Пусть мы зафиксировали некоторую клетку (i, j). Рассмотрим величину c = min(zlij, zldij). Это наибольший допустимый размер квадрата с верхним правым углом в (i, j). Теперь поймём сколько таких квадратов. Рассмотрим произвольную клетку (x, y) по диагонали вниз-влево на расстоянии не более c. Пара клеток (i, j) и (x, y) образует z-паттерн, если y + zrxy > j.
Отлично, теперь для решения задачи заведём структуру данных для каждой диагонали (она определяется формулой x + y), которая умеет прибавлять в точке и брать сумму на отрезке (лучше всего для этого подходит дерево Фенвика). Будем перебирать столбец j справа налево и обрабатывать события: некоторая клетка (x, y) такова, что y + zrxy - 1 = j. В этом случае нам нужно в дереве номер x + y сделать прибавление в точке y на единицу. Теперь будем перебирать клетку в текущем столбце (i, j). Тогда к ответу нужно прибавить величину суммы в дереве номер i + j на отрезке от j - c + 1 до j.
Сложность: O(nmlogm).
628F - Медведь и справедливое множество
Задача предложена и подготовлена Камилем Дебовски Errichto.
Вначале для удобства добавим подсказку с upTo = b, quantity = n, а затем отсортируем подсказки по значению upTo. Отсортированные подсказки разбивают интервал [1, b] на q непересекающихся промежутка. Для каждого промежутка мы знаем количество элементов в нём.
Для решения задачи построим сеть (описанную ниже) и найдём в ней максимальный поток. Ответ fair только если величина потока равна n.
- Первая группа вершин в сети A будет содержать 5 вершин, обозначающих возмоджные остатки.
- Вторая группа вершин B будет содержать q вершин, обозначающих промежутки.
Соединим каждую вершину из A с истоком ребром пропускной способности 
. Каждую вершину из B соединим со стоком ребром пропускной способности равной количеству чисел в этом промежутке. Между всему вершинами x из A и y из B добавим ребро пропускной способности равной количеству чисел в промежутке с остатком x в промежутке y.
Легко видеть, что поток в данной сети очень похож на паросочетание. В самом деле мы можем воспользоваться теоремой Холла. Для каждого из 25 множеств вершин из A (множества остатков) пройдём по всем промежуткам и посчитаем количество чисел, которые мы можем взять в [1, b] с остатками в заданном множестве.
Реализицая с теоремой Холла: C++ solution.
Сложность: O(2Cn), где в нашей задаче C = 5.
