To know how much water you consume per second you should divide consumed volume, v, by the area of the cup, 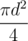 . Then you should compare thisit with e. If your speed of drinking is greater, then you'll drink all the water in
. Then you should compare thisit with e. If your speed of drinking is greater, then you'll drink all the water in 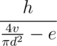 seconds. Otherwise you would never do it.
seconds. Otherwise you would never do it.
It is possible to make a convex polygon with given side lengths if and only if a generalized triangle inequality holds: the length of the longest side is less than the sum of lengths of other sides. It is impossible to make a convex polygon from a given set, so there is a side which is longest than (or equals to) than sum of others. Assume it is greater by k; then it is sufficient to add a rod of length k + 1. More, it is clear that adding any shorter length wouldn't satisfy the inequality. Thus the answer for the problem is  .
.
666A - Reberland Linguistics / 667C - Reberland Linguistics
This problem is solved with dynamic programming. We can select an arbitrary root of any length (at least five). Let's reverse the string. A boolean value dp2, 3[n] denotes if we could split a prefix of length n to a strings of length 2 and 3 so that the last string has a corresponding length. Transitions: 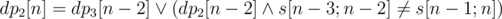 . Similarly,
. Similarly, 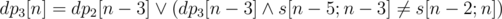 . If any of dpk[n] is true we add the corresponding string to the set of answers.
. If any of dpk[n] is true we add the corresponding string to the set of answers.
666B - World Tour / 667D - World Tour
You are given the oriented graph, find four distinct vertices a, b, c, d such that each vertex if reachable from previous and the sum of shortest paths between consequitive vertices is as large as possible. First let's run a BFS from each vertex and find three most distant vertices over given graph and its reverse. Afterwards loop through each possible b and c. Having them fixed, loop through a among three most distant vertices from b in the reversed graph and through d among three most distant vertices from c in tie initial graph. This is sufficient, because if we've fixed b and c and d is not one of three furthest from c then we could replace it with one of them and improve the answer.
The first thing to notice: string itself does not matter, only its length does. In each sequence of length n containing a fixed subsequence s we can select s's lexicographically minimal occurance, let it be p1, ..., p|s|. No character sk + 1 may occur between pk and pk + 1 - 1, because otherwise the occurence is not lex-min. On the other hand, if there is an occurence which satsfies this criterion than it is lex-min.
Given this definition we can count number of strings containing given string as a subsequence. At first select positions of the lex-min occurance; there are 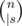 ways to do it. Next, you can use any of Σ - 1 characters at first s intervals between pi, and any of Σ at the end of the string. (Here, Σ denotes alphabet size).
ways to do it. Next, you can use any of Σ - 1 characters at first s intervals between pi, and any of Σ at the end of the string. (Here, Σ denotes alphabet size).
Looping through p|s| — the position of last character in s in the lex-min occurence, we can count that there are exactly 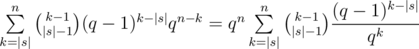 strings containing s as a subsequence. So, having |s| fixed, answer for each n could be computed in linear time.
strings containing s as a subsequence. So, having |s| fixed, answer for each n could be computed in linear time.
A final detail: input strings can have at most 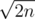 different lengths. Thus simply applying the overmentioned formula we get a
different lengths. Thus simply applying the overmentioned formula we get a  solution, which was the expected one.
solution, which was the expected one.
666D - Chain Reaction / 667E - Chain Reaction
You are given four points on the plain. You should move each of them up, down, left, or right, such that the new configuration is a square with positive integer sides parallel to coordinate axes.
Choose some d, length of the square side, and (x, y), the position of the bottom-left point. A set from where to choose will be constructed later. Then fix one of 24 permutations of initial points: first goes to the bottom-left point of the square, second goes to the bottom-right, etc. Having it fixed it is easy to check if this configuration is valid and relax the answer if needed. The only question is where to look for d, x and y.
First we deal with d. You can see that there are always two points which move among parallel but not the same lines. In this case d is the distance between these lines, i.e. one of |xi - xj| or |yi - yj|. This is the set from where d will be chosen.
Now fix d from the overmentioned set and look at two cases.
- There are two points moving by perpendicular lines. Then there is a square vertex in the point of these lines intersection. In each coordinate this point either equals to bottom-left point of the square or differs by exactly d. Thus if bottom-left point has coordinates (x0, y0), than x0 must be some of xi, xi + d, xi - d, similarly for y0. Add all this values to the set.
- All points are moving among parallel lines; WLOG horisontal. Let's fix a permutation of points (yes, once again) and shift each point in such a way that after moving it would equal the bottom-left vertex of the square. Second point should be shifted by ( - d, 0), third by (0, - d), fourth by ( - d, - d). All four points must be on the same line now; otherwise this case is not possible with this permutation. Now the problem is: given four points on a line, move it to the same point minimizing the maximal path. Clearly, one should move points to the position (maxX - minX) / 2; rounding is irrelevant because of the constraint of integer answer. So, having looked through each permutations, we have another set for bottom-left vertex possible coordinates.
By the way, the 10th test (and the first test after pretests) was case 2; it was intentionally not included in pretests.
Why does it work fast? Let D and X be the sizes of corresponding lookup sets. 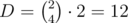 . Now for each d there are 4·3 = 12 coordinates in the first case and no more than 4! = 24 in the second. Thus X ≤ 12·(12 + 24) = 432. The main part works in
. Now for each d there are 4·3 = 12 coordinates in the first case and no more than 4! = 24 in the second. Thus X ≤ 12·(12 + 24) = 432. The main part works in 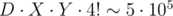 ; however, it is impossible to build a test where all permutations in the second case give a valid position, so you can reduce this number. Actually, the model solution solves 50 testcases in 10ms without any kind of pruning.
; however, it is impossible to build a test where all permutations in the second case give a valid position, so you can reduce this number. Actually, the model solution solves 50 testcases in 10ms without any kind of pruning.
You are given string s and m strings ti. Queries of type ``find the string ti with number from [l;r] which has the largest amount of occurrences of substring s[a, b]'' approaching. Let's build segment tree over the texts t_i. In each vertex of segment tree let's build suffix automaton for the concatenation of texts from corresponding segment with delimeters like a#b. Also for each state in this automaton we should found the number of text in which this state state occurs most over all texts from the segment. Also for each state v in this automaton we should find such states in children of current segment tree vertex that include the set of string from v. If you maintain only such states that do not contain strings like a#b, it is obvious that either wanted state exists or there is no occurrences of strings from v in the texts from child's segment at all. Thus, to answer the query, firstly we find in root vertex the state containing string s[a;b], and after this we go down the segment tree keeping the correct state via links calculated from the previous state.
Please refer to the code if something is unclear.






