Short problem statement: Given T < 200 binary strings S (|S| ≤ 105), find the size of the shortest pattern that doesn't match S for all input strings.
Examples :
S = 011101001, answer = 3 (doesnt match '000')
S = 11111, answer = 1 (doesnt match '0')
My current solution is building a suffix automaton for S and searching all patterns of size i (i=1, i=2, ...) while the number of matches of this size equals 2i. When i find some k such that matches(k) < 2k, this is the answer. This is O(|S|) for building suffix automata plus 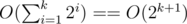 for matchings, which i think is always small but still relevant.
for matchings, which i think is always small but still relevant.
This solution gets TLE. Can anyone help me with a faster solution for this problem? Thanks in advance.
EDIT 2: Solved the problem using the strategy below. I will leave the blog here any way because this problem looks interesting so i want to share the solution in case any one is interested :)
Run BFS in suffix automata starting from root node until we find some node that has less than 2 links. Let p be the length of the path from root to this node. This node represents some pattern of length p+1 that doesn't appear in the string S. So the answer is p+1.






