Given a bipartite graph with nonnegative edge weights, find a matching with maximum total weight (maximum number of edges is not required).
Example:
V = {1, 2, 3, 4}, E = {{1, 2}, {3, 4}, {2, 3}}
w({1, 2}) = 1, w({3, 4}) = 1, w({2, 3}) = 10
Optimal solution: {{2, 3}}
A friend suggested the following solution:
- Ignore weights and find maximum cardinality bipartite matching MCBM.
- For each
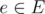 , define w'(e) = BIGVALUE - w(e).
, define w'(e) = BIGVALUE - w(e). - Find mincost flow for f = 1, 2, 3, ..., MCBM with respect to new weight function w'. Output the minimum.
Will that work? Is there any faster solution?






