757A — Gotta Catch Em' All!
Author: Baba
Testers: virus_1010 born2rule
Expected complexity: 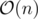
Main idea: Maintain counts of required characters.
Since we are allowed to permute the string in any order to find the maximum occurences of the string "Bulbasaur", we simply keep the count of the letters 'B', 'u', 'l', 'b', 'a', 's', 'r'. Now the string "Bulbasaur" contains 1 'B', 2'u', 1 'l', 2'a', 1 's', 1'r' and 1 'b', thus the answer to the problem is Min(count('B'), count('b'), count('s'), count('r'), count('l'), count('a')/2, count('u')/2). You can maintain the counts using an array.
Corner Cases:
1. Neglecting 'B' and while calculating the answer considering count('b')/2.
2. Considering a letter more than once ( 'a' and 'u' ).
757B — Bash's Big Day
Author: architrai
Testers: mprocks, deepanshugarg
Expected complexity: 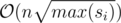
Main idea: Square-root factorization and keeping count of prime factors.
The problem can be simplified to finding a group of Pokemons such that their strengths have a common factor other that 1. We can do this by marking just the prime factors, and the answer will be the maximum count of a prime factor occurring some number of times. The prime numbers of each number can be found out using pre-computed sieve or square-root factorization.
Corner Cases : Since a Pokemon cannot fight with itself (as mentioned in the note), the minimum answer is 1. Thus, even in cases where every subset of the input has gcd equal to 1, the answer will be 1.
757C — Felicity is Coming!
Author: shivamkakkar
Testers: codelegend
Expected complexity: 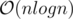
Main idea: Divide pokemon types into equivalence classes based on their counts in each list.
Consider a valid evolution plan f. Let c[p, g] be the number of times Pokemon p appears in gym g. If f(p) = q then 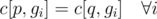 .
.
Now consider a group of Pokemon P such that all of them occur equal number of times in each gym (i.e. for each 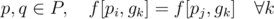 ). Any permutation of this group would be a valid bijection.
). Any permutation of this group would be a valid bijection.
Say we have groups s1, s2, s3, ..., then the answer would be |s1|! |s2|! |s3|! ... mod 109 + 7.
For implementing groups, we can use vector < vector < int > > and for i-th pokemon, add the index of the gym to i-th vector.
Now we need to find which of these vectors are equal. If we have the sorted vector < vector < int > > , we can find equal elements by iterating over it and comparing adjacent elements.
Consider the merge step of merge sort. For a comparison between 2 vectors v1 and v2, we cover at least min(v1.size(), v2.size()) elements. Hence 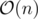 work is done at each level. There are
work is done at each level. There are 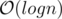 levels.
levels.
Bonus : Try proving the time complexity for quicksort as well.
757D — Felicity's Big Secret Revealed
Author: saatwik27
Testers: imamit,abhinavaggarwal,Chipe1
This problem can be solved using Dynamic Programming with bitmask.
The important thing to note here is that the set of distinct numbers formed will be a maximum of 20 numbers, i.e. from 1 to 20, else it won't fit 75 bits(1*(1 bits) + 2*(2 bits) + 4*(3 bits) + 8*(4 bits) + 5*(5 bits) = 74 bits). So, we can use a bitmask to denote a set of numbers that are included in a set of cuts.
Let's see a Top-Down approach to solve it :
Lets define the function f(i, mask) as : f(i, mask) denotes the number of sets of valid cuts that can be obtained from the state i, mask. The state formation is defined below.
Let M be the maximum number among the numbers in mask. mask denotes a set of numbers that have been generated using some number of cuts, all of them before bi. Out of these cuts, the last cut has been placed just before bi. Now, first we check if the set of cuts obtained from mask is valid or not(in order for a mask to be valid, mask == 2X - 1 where X denotes number of set bits in the mask) and increment the answer accordingly if the mask is valid. And then we also have the option of adding another cut. We can add the next cut just before bx provided the number formed by "bi bi + 1...bx - 1" <= 20. Set the corresponding bit for this number formed to 1 in the mask to obtain newMask and recursively find f(x, newMask).
757E — Bash Plays with Functions
Author: satyam.pandey
Testers: Superty,vmrajas
We can easily see that f0 = 2(number of distinct prime factors of n). We can also see that it is a multiplicative function.
We can also simplify the definition of fr + 1 as:
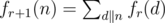
Since f0 is a multiplicative function, fr + 1 is also a multiplicative function. (by property of multiplicative functions)
For each query, factorize n.
Now, since fr is a multiplicative function, if n can be written as:
Then fr(n) can be computed as:
Now observe that the value of fr(pn) is independent of p, as f0(pn) = 2. It is dependent only on n. So we calculate fr(2x) for all r and x using a simple R * 20 DP as follows:
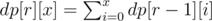
And now we can quickly compute fr(n) for each query as:
757F — Team Rocket Rises Again
Author: Baba
Testers: shubhamvijay, tanmayc25, vmrajas
Expected complexity: 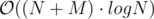
Main idea: Building Dominator tree on shortest path DAG.
First of all, we run Dijkstra's shortest path algorithm from s as the source vertex and construct the shortest path DAG of the given graph. Note that in the shortest path DAG, the length of any path from s to any other node x is equal to the length of the shortest path from s to x in the given graph.
Now, let us analyze what the function f(s, x) means. It will be equal to the number of nodes u such that every path from s to u passes through node x in the shortest path DAG, such that on removing node x from the DAG, there will be no path from s to u.
In other words, we want to find the number of nodes u that are dominated by node x considering s as the sources vertex in the shortest path DAG. This can be calculated by building dominator tree of the shortest path DAG considering s as the source vertex.
A node u is said to dominate a node w wrt source vertex s if all the paths from s to w in the graph must pass through node u.
You can read more about dominator tree here.
Once the dominator tree is formed, the answer for any node x is equal to the number of nodes in the subtree of x in the tree formed.
Another approach for forming dominator tree is by observing that the shortest path directed graph formed is a DAG i.e. acyclic. So suppose we process the nodes of the shortest path dag in topological order and have a dominator tree of all nodes from which we can reach x already formed. Now, for the node x, we look at all the parents p of x in the DAG, and compute their LCA in the dominator tree built till now. We can now attach the node x as a child of the LCA in the tree.
For more details on this approach you can look at jqdai0815's solution here.
757G — Can Bash Save the Day?
Author: Baba
Testers: Toshad, abhinavaggarwal
Expected complexity: 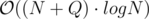
Main idea: Making the Centroid Tree Persistent.
Simpler Problem
First let's try to solve a much simpler problem given as follows.
Question: Given a weighted tree, initially all the nodes of the given tree are inactive. We need to support the following operations fast :
Query v : Report the sum of distances of all active nodes from node v in the given tree.
Activate v : Mark node v to be an active node.
Solution: The above problem can be easily solved by a fairly standard technique called Centroid Decomposition. You can read more about here
Solution Idea
- Each query of the form (L R v) can be divided into two queries of form (1 R v) - (1 L - 1 v). Hence it is sufficient if we can support the following query: (i v) : Report the answer to query (1 i v)
- To answer a single query of the form (i v) we can think of it as what is the sum of distance of all active nodes from node v, if we consider the first i nodes to be active.
- Hence initially if we can preprocess the tree such that we activate nodes from 1 to n and after each update, store a copy of the centroid tree, then for each query (i v) we can lookup the centroid tree corresponding to i, which would have the first i nodes activated, and query for node v in
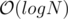 time by looking at it’s ancestors.
time by looking at it’s ancestors. - To store a copy of the centroid tree for each i, we need to make it persistent.
Persistent Centroid Tree : Key Ideas
- Important thing to note is that single update in the centroid tree affects only the ancestors of the node in the tree.
- Since height of the centroid tree is
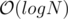 , each update affects only
, each update affects only 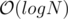 other nodes in the centroid tree.
other nodes in the centroid tree. - The idea is very similar to that of a persistent segment tree BUT unlike segtree, here each node of the centroid tree can have arbitrarily many children and hence simply creating a new copy of the affected nodes would not work because linking them to the children of old copy would take
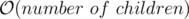 for each affected node and this number could be as large as N, hence it could take
for each affected node and this number could be as large as N, hence it could take  time in total !
time in total !
Binarizing the Input Tree
- To overcome the issue, we convert the given tree T into an equivalent binary tree T' by adding extra dummy nodes such that degree of each node in the transformed tree T' is < = 3, and the number of dummy nodes added is bounded by
 .
. - The dummy nodes are added such that the structure of the tree is preserved and weights of the edges added are set to 0.
- To do this, consider a node x with degree d > 3 and let c1, c2...cd be it's adjacent nodes. Add a new node y and change the edges as follows :
- Delete the edges (x - c3), (x - c4) ... (x - cd) and add the edge (x - y) such that degree of node x reduces to 3 from d.
- Add edges (y - c3), (y - c4) ... (y - cd) such that degree of node y is d - 1. Recursively call the procedure on node y.
- Since degree of node y is d - 1 instead of original degree d of node x, it can be proved that we need to add at most
 new nodes before degree of each node in the tree is < = 3.
new nodes before degree of each node in the tree is < = 3.
Conclusion
Hence we perform centroid decomposition of this transformed tree T'. The centroid tree formed would have the following properties.
- The height of the centroid tree is
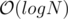
- Each node in the centroid tree has ≤ 3 children.
Now we can easily make this tree persistent by path-copying approach.
To handle the updates,
- Way-1 : Observe that swapping A[i] and A[i + 1] would affect only the i'th persistent centroid tree, which can be rebuilt from the tree of i - 1 by a single update query. In this approach, for each update we add
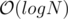 new nodes. See author's code below for more details.
new nodes. See author's code below for more details. - Way-2 : First we go down to the lca of A[x] and A[x + 1] in the x'th persistent tree, updating the values as we go. Now, let cl be the child of lca which is an ancestor of A[x], and let cr be the child which is an ancestor of A[x + 1]. Now, we replace cr of x'th persistent tree with cr of (x + 1)'th persistent tree. Similarly, we replace cl of x + 1'th persistent tree with cl of x'th persistent tree. So now A[x + 1] is active in x'th persistent tree and both A[x] and A[x + 1] are active in (x + 1)'th persistent tree.To deactivate A[x] in x'th persistent tree we replace cl of x'th persistent tree with cl of (x - 1)'th persistent tree. Hence in this approach we do not need to create new
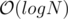 nodes for each update. See testers's code below for more details.
nodes for each update. See testers's code below for more details.
Hope you enjoyed the problemset! Any feedback is appreciatd! :)






