Weekly Training Farm 22 — Editorial

Правка en1, от zscoder, 2017-01-20 16:33:43

Weekly Training Farm 22 is over. Congratulations to the winners :

  1. W4yneb0t (perfect score in < 1 hour!)

  2. aaaaajack (perfect score)

  3. eddy1021

Here is the editorial :

Problem A

This problem can be solved by greedy. We list down the positive integers one by one. We keep a pointer that initially points to the first letter of s. Whenever the pointed character in the string s matches the corresponding digit of the integer, we move the pointer one step to the right and continue. Repeat this process until the pointer reaches the end.

However, we still need to know whether the answer can be large. The key is to note that the answer will never exceed 106, because after writing down 10 consecutive numbers, at least one of them has last digit equals to the current digit, so the pointer will move to the right at least once when we write down 10 consecutive numbers. Thus, in the worse case, we'll only list down the numbers from 1 to 106, which is definitely fast enough.

Code

Problem B

This problem can be solved using dynamic programming. Firstly, observe that if we already determine which set of problems to solve, then it's best to solve the problem in increasing order of time needed to solve in order to minimize the time penalty. Thus, we can first sort the problems in increasing order of time needed, breaking ties arbitarily.

Let dp[i][j] denote the maximum number of problems solved and minimum time penalty acquired when doing so by using exactly j minutes and only solving problems among the first i ones. dp[0][0] = (0, 0) (the first integer denotes the number of problems solved and the second integer denotes the time penalty in order to do so). The transitions can be handled easily by simply considering whether to solve the i-th problem or not. The time complexity of this solution is O(nT) (T is the duration of the contest)

Code

Problem C

This is an ad hoc problem. Firstly, we can use two moves to determine what the value of the first bit is. (simply flipping it twice will tell you its value. Now, if the bit is 1, you don't need to flip it anymore. If it's 0, you'll need to flip it. In any case, we'll flip the second bit as well. (if the first bit needs to be flipped, we'll flip [1, 2] and flip [2, 2] otherwise) After flipping the second bit, we can determine whether it's a 1 or 0 by calculating from the total number of 1s of the string before the flip and after the flip. We can repeat this for every 2 consecutive bits until we arrive at the last two bits. At this point, we know what the second last bit is, and we also know the total number of 1 bits. So, we can easily deduce the value of the last bit from the information as well. Now, we just need to perform one last flip to make the last 2 bits become 1. The total number of moves made is n + 1.

Code

Problem D1

First, we can use 18 moves to determine the value of a, by asking 2 to 19 in increasing order and the first yes answer will be the value of a. If there're no "yes" answers, then the value of a is 20.

Call a number good if it can be represented as the sum of nonnegative multiples of as and b. Note that if x is good, then x + a, x + b are both good.

Now that we have the value of a, let's think about what b is. Consider the numbers ka + 1, ka + 2, ..., ka + (a - 1) for a fixed k. If none of these numbers are good, we can immediately say that b is larger than (k + 1)a. Why? Suppose b = qa + r. Clearly, r ≠ 0 since a and b are coprime. Note that xa + r for all x ≥ q will be the good, since xa + r = (qa + r) + (x - q)a = b + (x - q)a. So, b cannot be less than any of the numbers ka + 1, ka + 2, ..., ka + (a - 1), or else one of these numbers would've been good, a contradiction. Note that this also means that if y is the smallest integer such that ya + 1, ya + 2, ..., ya + (a - 1) are not all bad, then there will be exactly one good number, which will be b. Also note that for all integers k > y, there will have at least one good number among ka + 1, ka + 2, ..., ka + (a - 1). Thus, we can now binary search for the value of y. In each iteration of the binary search, we need to ask at most a - 1 ≤ 19 questions, and there are at most 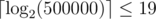iterations, so the maximum number of operations needed is 19·19 + 18 = 379 < 380.

Code

Problem D2

This problem is the same as D1, but with higher constraints. Firstly, we find the value of a in 18 moves as in problem D. To proceed, we need to think about this problem from another angle. Suppose we know a number N that is good and not a multiple of a, and we can find the maximum number k such that N - ka is good, then what does this tell us? This means that N - ka is a multiple of b. Why? We know that N - ka = ax + by for some nonnegative integers x and y since N - ka is good. If x > 0, then N - (k + 1)a = a(x - 1) + by is also good, contradicting the maximality of k. Thus, x = 0 and so N - ka = by. Note that b > 0 since we choose N so that it's not a multiple of a.

To find a value of N such that N is good and not a multiple of a, it is sufficient to take 500000a - 1, since any number greater than ab - a - b is guaranteed to be good. (this is a well-known fact)

We can find the largest k such that N - ka is good via binary search, because if N - ma is not good then N - (m + 1)a can't be good. (or else if N - (m + 1)a = ax + by, then N - ma = a(x + 1) + by) This takes at most 19 questions.

What to do after finding a value which is a multiple of b? Let C = N - ka. We consider the prime factorization of C. The main claim is that if 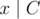is good, then x must be a multiple of b. The reasoning is the same as what we did before. So, we can find the prime factorization of C, and divide the prime factors one by one. If the number becomes bad, we know that the prime factor cannot be removed, and proceed to the next prime factor. Since a number less than 500000 can have at most 18 prime factors (maximum is 218), so this takes another 18 questions.

Thus, we only used 18 + 19 + 18 = 55 < 60 questions to find the values of a and b.

Code

Problem E

Firstly, note that a connected graph on n vertices with n edges contains exactly 1 cycle. Call the vertices on the cycle the cycle vertices. From each cycle vertex, there's a tree rooted at it. Thus, call the remaining vertices the tree vertices. Note that the number of useless edges is equal to the length of the cycle.

Now, we do some casework :

  • u is equal to a tree vertex

Note that this will not change the length of the cycle. Thus, we just have to count how many ways are there to change the value of au such that the graph remains connected. The observation is that for each tree node u, the only possible values of au are the nodes which are not in the subtree of u in the tree u belongs to. Thus, the number of possibilities can be calculated with a tree dp. For each tree, we calculate the subtree size of each node and add all these subtree sizes and subtract this from the total number of ways to choose a non-tree vertex u and choosing the value of au. This part can be done in O(n) time.

  • u is equal to a cycle vertex

For two cycle vertices u and v, let d(u, v) be the directed distance from u to v (We consider the distance from u to v in the functional graph 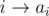for all 1 ≤ i ≤ n). Note that if we change au to x, and the root of the tree x is in is v (x = v is x is a cycle vertex), then the length of the cycle after the change will be d(v, u) + 1 + h[x], where h[x] is the height of x in its tree. The key is instead of fixing u and iterate through all other nodes x, we iterate through all endpoints x and see how it changes our answer. Note that if x is fixed, which also means that v is fixed, then we just have to add 1 to the answer for c = d(v, u) + 1 + h[x] for all cycle vertices u. However, note that d(v, u) ranges from 0 to C - 1 (where C denotes the length of the original cycle), so this is equivalent to adding 1 to the answer for c = h[x] + 1, h[x] + 2, ..., h[x] + C. Now, we can iterate through all vertices x and add 1 to the answer for c = h[x] + 1, h[x] + 2, ..., h[x] + C. To do this quickly, we can employ the "+1, -1" method. Whenever we want to add 1 to a range [l, r], we add 1 to ansl and subtract 1 from ansr + 1. Then, to find the actual values of the ans array, we just have to take the prefix sum of the ans array.

Finally, do not forget to subtract the cases where v = au from the answer. The total complexity is O(n).

Code
Теги weekly training farm

История

 
 
 
 
Правки
 
 
  Rev. Язык Кто Когда Δ Комментарий
en2 Английский zscoder 2017-01-20 16:44:50 33
en1 Английский zscoder 2017-01-20 16:33:43 21213 Initial revision (published)