This is an editorial for the problems of the today's contest. I tried my best to describe the solutions for the problems as detailed as possible, but if something is not understandable for you, you can write in comments! :)
404 Not Found
#include <iostream>
#include <map>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
map<string, int> vals;
vals["Tetrahedron"] = 4;
vals["Cube"] = 6;
vals["Octahedron"] = 8;
vals["Dodecahedron"] = 12;
vals["Icosahedron"] = 20;
int n; cin >> n;
int res = 0;
for (int i = 0; i < n; i++) {
string s; cin >> s;
res += vals[s];
}
cout << res << endl;
return 0;
}
import java.io.*;
import java.util.*;
public class PolyhedronSums {
public static void main(String[] args) throws Exception {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
HashMap<String, Integer> vals = new HashMap<String, Integer>();
vals.put("Tetrahedron", 4);
vals.put("Cube", 6);
vals.put("Octahedron", 8);
vals.put("Dodecahedron", 12);
vals.put("Icosahedron", 20);
int n = Integer.parseInt(reader.readLine());
int res = 0;
for (int i = 0; i < n; i++) {
res += vals.get(reader.readLine());
}
writer.write(Integer.toString(res));
reader.close();
writer.close();
}
}
vals = {
'Tetrahedron': 4,
'Cube': 6,
'Octahedron': 8,
'Dodecahedron': 12,
'Icosahedron': 20
}
n = int(input())
ans = 0
for i in range(0, n):
ans += vals[input()]
print(ans)
Think of what periods to take if Anton attends chess classes earlier than programming classes and vice versa.
#include <iostream>
#include <algorithm>
const int infinity = 1234567890;
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
int n; cin >> n;
vector<pair<int, int> > a(n);
for (int i = 0; i < n; i++) {
cin >> a[i].first >> a[i].second;
}
int m; cin >> m;
vector<pair<int, int> > b(m);
for (int i = 0; i < m; i++) {
cin >> b[i].first >> b[i].second;
}
int minR1 = infinity, maxL1 = -infinity;
int minR2 = infinity, maxL2 = -infinity;
for (int i = 0; i < n; i++) {
maxL1 = max(maxL1, a[i].first);
minR1 = min(minR1, a[i].second);
}
for (int i = 0; i < m; i++) {
maxL2 = max(maxL2, b[i].first);
minR2 = min(minR2, b[i].second);
}
int res = max(maxL2 - minR1, maxL1 - minR2);
cout << max(res, 0) << endl;
return 0;
}
import java.io.*;
import java.util.*;
public class TwoSegments {
public static final int infinity = 1234567890;
public static class Segment {
public int l;
public int r;
public Segment(int aL, int aR) {
l = aL;
r = aR;
}
}
private static Segment[] readList(BufferedReader reader) throws Exception {
int n = Integer.parseInt(reader.readLine());
Segment[] res = new Segment[n];
for (int i = 0; i < n; i++) {
StringTokenizer tokenizer = new StringTokenizer(reader.readLine());
int l = Integer.parseInt(tokenizer.nextToken());
int r = Integer.parseInt(tokenizer.nextToken());
res[i] = new Segment(l, r);
}
return res;
}
public static void main(String[] args) throws Exception {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
Segment[] a = readList(reader);
Segment[] b = readList(reader);
int minR1 = infinity, maxL1 = -infinity;
int minR2 = infinity, maxL2 = -infinity;
for (int i = 0; i < a.length; i++) {
maxL1 = Math.max(maxL1, a[i].l);
minR1 = Math.min(minR1, a[i].r);
}
for (int i = 0; i < b.length; i++) {
maxL2 = Math.max(maxL2, b[i].l);
minR2 = Math.min(minR2, b[i].r);
}
int res = Math.max(maxL2 - minR1, maxL1 - minR2);
writer.write(Integer.toString(Math.max(res, 0)));
reader.close();
writer.close();
}
}
infinity = 1234567890
minR1 = minR2 = infinity
maxL1 = maxL2 = -infinity
n = int(input())
for i in range(0, n):
(l, r) = map(int, input().split())
maxL1 = max(maxL1, l)
minR1 = min(minR1, r)
m = int(input())
for i in range(0, m):
(l, r) = map(int, input().split())
maxL2 = max(maxL2, l)
minR2 = min(minR2, r)
res = max(maxL2 - minR1, maxL1 - minR2);
print(max(res, 0))
This problem had weak pretests. It was made intentionally to cause more hacks. And I have warned you about it in the announcement :)
Model the process to determine how the number of corns in the barn changes.
#include <iostream>
#include <cstdint>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
int64_t n, m;
cin >> n >> m;
if (n <= m) {
cout << n << endl;
} else {
n -= m;
int64_t l = 0, r = 2e9;
while (l < r) {
int64_t m = (l + r) / 2;
int64_t val = m * (m+1) / 2;
if (val >= n) {
r = m;
} else {
l = m+1;
}
}
cout << l + m << endl;
}
return 0;
}
import java.io.*;
import java.util.*;
public class SparrowsJava {
public static void main(String[] args) throws Exception {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer tokenizer = new StringTokenizer(reader.readLine());
long n = Long.parseLong(tokenizer.nextToken());
long m = Long.parseLong(tokenizer.nextToken());
if (n <= m) {
writer.write(Long.toString(n));
} else {
n -= m;
long l = 0, r = (long)2e9;
while (l < r) {
long med = (l + r) / 2;
long val = med * (med+1) / 2;
if (val >= n) {
r = med;
} else {
l = med+1;
}
}
writer.write(Long.toString(l + m));
}
reader.close();
writer.close();
}
}
(n, m) = map(int, input().split())
if n <= m:
print(n)
else:
aM = m
n -= m
(l, r) = (0, int(2e9))
while l < r:
m = (l + r) // 2;
val = m * (m+1) // 2;
if val >= n:
r = m
else:
l = m+1
print(l + aM)
Solve a simplified version of the problem. Let our sequence first contains x opening brackets and then contains y closing brackets, and the last opening bracket must necessarily appear in our RSBS. Use a naive solution to see how the answer looks. Think what to do next.
#include <iostream>
#include <vector>
#include <cstdint>
using namespace std;
int mod = (int)1e9 + 7;
int64_t extGcd(int64_t a, int64_t b, int64_t& x, int64_t& y) {
if (!a) {
x = 0;
y = 1;
return b;
}
int64_t x1, y1;
int64_t d = extGcd(b % a, a, x1, y1);
x = y1 - (b / a) * x1;
y = x1;
return d;
}
inline int addMod(int a, int b, int m = mod) {
return ((int64_t)a + b) % m;
}
inline int mulMod(int a, int b, int m = mod) {
return ((int64_t)a * b) % m;
}
inline int divMod(int a, int b, int m = mod) {
int64_t x, y;
int64_t g = extGcd(b, m, x, y);
if (g != 1) {
cerr << "Bad gcd!" << endl;
for (;;);
}
x = (x % m + m) % m;
return mulMod(a, x, m);
}
const int factRange = 1000000;
int fact[factRange];
inline void precalcFactorials() {
fact[0] = 1;
for (int i = 1; i < factRange; i++) {
fact[i] = mulMod(fact[i-1], i);
}
}
inline int F(int n) {
return (n < 0) ? 0 : fact[n];
}
inline int C(int k, int n) {
return divMod(F(n), mulMod(F(n-k), F(k)));
}
int main() {
ios_base::sync_with_stdio(false);
string s;
cin >> s;
int len = s.size();
precalcFactorials();
vector<int> opnLeft(len), clsRight(len);
opnLeft[0] = (s[0] == '(') ? 1 : 0;
for (int i = 1; i < len; i++) {
opnLeft[i] = opnLeft[i-1] + ((s[i] == '(') ? 1 : 0);
}
clsRight[len-1] = (s[len-1] == ')') ? 1 : 0;
for (int i = len-2; i >= 0; i--) {
clsRight[i] = clsRight[i+1] + ((s[i] == ')') ? 1 : 0);
}
int res = 0;
for (int i = 0; i < len; i++) {
if (s[i] != '(' || clsRight[i] == 0) {
continue;
}
int add = C(opnLeft[i], opnLeft[i] + clsRight[i] - 1);
res = addMod(res, add);
}
cout << res << endl;
return 0;
}
import java.io.*;
import java.util.*;
public class BracketsJava {
public static int mod = (int)1e9 + 7;
public static class ExtGcdResult {
long x;
long y;
}
public static long extGcd(long a, long b, ExtGcdResult res) {
if (a == 0) {
res.x = 0L;
res.y = 1L;
return b;
}
ExtGcdResult newRes = new ExtGcdResult();
long d = extGcd(b % a, a, newRes);
res.x = newRes.y - (b / a) * newRes.x;
res.y = newRes.x;
return d;
}
public static final int addMod(int a, int b) {
return (int)(((long)a + b) % mod);
}
public static final int mulMod(int a, int b) {
return (int)(((long)a * b) % mod);
}
public static final int divMod(int a, int b) {
ExtGcdResult res = new ExtGcdResult();
long g = extGcd(b, mod, res);
if (g != 1) {
System.out.println("Bad gcd!");
for (;;);
}
int q = (int)((res.x % mod + mod) % mod);
return mulMod(a, q);
}
public static final int[] precalcFactorials() {
int[] fact = new int[factRange];
fact[0] = 1;
for (int i = 1; i < factRange; i++) {
fact[i] = mulMod(fact[i-1], i);
}
return fact;
}
public static final int factRange = 1000000;
public static final int[] fact = precalcFactorials();
public static final int F(int n) {
return (n < 0) ? 0 : fact[n];
}
public static final int C(int k, int n) {
int res = divMod(F(n), mulMod(F(n-k), F(k)));
return divMod(F(n), mulMod(F(n-k), F(k)));
}
public static void main(String[] args) throws Exception {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
String s = reader.readLine();
int len = s.length();
int[] opnLeft = new int[len], clsRight = new int[len];
opnLeft[0] = (s.charAt(0) == '(') ? 1 : 0;
for (int i = 1; i < len; i++) {
opnLeft[i] = opnLeft[i-1] + ((s.charAt(i) == '(') ? 1 : 0);
}
clsRight[len-1] = (s.charAt(len-1) == ')') ? 1 : 0;
for (int i = len-2; i >= 0; i--) {
clsRight[i] = clsRight[i+1] + ((s.charAt(i) == ')') ? 1 : 0);
}
int res = 0;
for (int i = 0; i < len; i++) {
if (s.charAt(i) != '(' || clsRight[i] == 0) {
continue;
}
int add = C(opnLeft[i], opnLeft[i] + clsRight[i] - 1);
res = addMod(res, add);
}
writer.write(Integer.toString(res));
reader.close();
writer.close();
}
}
I'm sorry that this problem was not original. I will try my best to prevent this from happening again.
If you have TL or ML in this problem, don't think that the time/memory limits are too strict. The model solution works in 1.2 seconds and consumes 9 MB memory.
Divide all the queries in 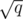 blocks. Then divide the positions to the mobile (those ones that will change in this block) and immoblile. Think what to do next.
blocks. Then divide the positions to the mobile (those ones that will change in this block) and immoblile. Think what to do next.
// Thanks to netman for the idea for this wonderful solution :)
#include <iostream>
#include <fstream>
#include <vector>
#include <cstdint>
#include <algorithm>
using namespace std;
class SQRTDecomposition {
private:
int n, sz;
vector<int> val;
vector<int> blocks;
public:
inline void add(int v, int delta) {
val[v] += delta;
blocks[v / sz] += delta;
}
inline int sum(int l, int r) {
if (l < 0) {
l = 0;
}
if (r >= n) {
r = n;
}
r++;
int res = 0;
int lBlock = (l + sz - 1) / sz, rBlock = r / sz;
for (int i = lBlock; i < rBlock; i++) {
res += blocks[i];
}
int lBlockR = lBlock * sz, rBlockR = rBlock * sz;
if (lBlockR >= rBlockR) {
for (int i = l; i < r; i++) {
res += val[i];
}
} else {
for (int i = l; i < lBlockR; i++) {
res += val[i];
}
for (int i = rBlockR; i < r; i++) {
res += val[i];
}
}
return res;
}
inline void clear() {
val.assign(val.size(), 0);
blocks.assign(blocks.size(), 0);
}
SQRTDecomposition(int n, int sz)
: n(n), sz(sz), val(n, 0), blocks((n + sz - 1) / sz, 0) {
}
};
struct ToProcess {
int x, y1, y2, sgn, id;
};
const int BLOCK_SZ_Q = 256;
const int BLOCK_SZ_N = 512;
const int MAX_N = 200000;
int n, q;
vector<ToProcess> sortedL[MAX_N], sortedR[MAX_N];
SQRTDecomposition sum(MAX_N, BLOCK_SZ_N);
int64_t ans[MAX_N], preAns[MAX_N];
pair<int, int> queries[MAX_N];
vector<int> goods;
int p[MAX_N];
bool good[MAX_N];
inline void add(int q, int sgn, int id) {
if (q-1 >= 0) {
sortedL[q-1].push_back({q-1, p[q]+1, n-1, sgn, id});
}
if (q+1 < n) {
sortedR[q+1].push_back({q+1, 0, p[q]-1, sgn, id});
}
}
int main() {
ios_base::sync_with_stdio(false);
cin >> n >> q;
for (int i = 0; i < n; i++) {
p[i] = i;
}
for (int i = 0; i < q; i++) {
cin >> queries[i].first >> queries[i].second;
queries[i].first--; queries[i].second--;
}
int64_t cnt = 0;
for (int i = 0; i < q; i += BLOCK_SZ_Q) {
int iEnd = min(q, i + BLOCK_SZ_Q);
for (int j = 0; j < n; j++) {
good[j] = false;
}
for (int j = i; j < iEnd; j++) {
good[queries[j].first] = true;
good[queries[j].second] = true;
}
goods.clear();
for (int j = 0; j < n; j++) {
if (good[j]) {
goods.push_back(j);
}
}
int64_t goodCnt = 0;
for (int j = 0; j < n; j++) {
sortedL[j].clear();
sortedR[j].clear();
}
for (int j = i; j < iEnd; j++) {
int a = queries[j].first, b = queries[j].second;
if (a == b) {
ans[j] += goodCnt;
continue;
}
for (int k = 0; k < (int)goods.size(); k++) {
int q = goods[k];
if (q == a || q == b) {
continue;
}
if ((p[q] < p[a] && q > a) ||
(p[q] > p[a] && q < a)) {
goodCnt--;
}
if ((p[q] < p[b] && q > b) ||
(p[q] > p[b] && q < b)) {
goodCnt--;
}
if ((p[q] < p[b] && q > a) ||
(p[q] > p[b] && q < a)) {
goodCnt++;
}
if ((p[q] < p[a] && q > b) ||
(p[q] > p[a] && q < b)) {
goodCnt++;
}
}
if ((a < b && p[a] > p[b]) ||
(a > b && p[a] < p[b])) {
goodCnt--;
} else {
goodCnt++;
}
ans[j] += goodCnt;
add(a, -1, j);
add(b, -1, j);
swap(p[a], p[b]);
add(a, +1, j);
add(b, +1, j);
}
sum.clear();
for (int j = 0; j < n; j++) {
if (!good[j]) {
sum.add(p[j], 1);
}
for (int k = 0; k < (int)sortedL[j].size(); k++) {
ToProcess &cur = sortedL[j][k];
int64_t res = sum.sum(cur.y1, cur.y2);
res *= cur.sgn;
preAns[cur.id] += res;
}
}
sum.clear();
for (int j = n-1; j >= 0; j--) {
if (!good[j]) {
sum.add(p[j], 1);
}
for (int k = 0; k < (int)sortedR[j].size(); k++) {
ToProcess &cur = sortedR[j][k];
int64_t res = sum.sum(cur.y1, cur.y2);
res *= cur.sgn;
preAns[cur.id] += res;
}
}
for (int j = i; j < iEnd; j++) {
if (j != i) {
preAns[j] += preAns[j-1];
}
ans[j] += cnt + preAns[j];
}
cnt = ans[iEnd - 1];
}
for (int i = 0; i < q; i++) {
cout << ans[i] << "\n";
}
return 0;
}
import java.io.*;
import java.util.*;
public class InversionNSqrtNNoVectors {
private static final int BLOCK_SZ_Q = 256;
private static final int BLOCK_SZ_N = 512;
public static class ToProcess {
public int x, y1, y2, sgn, id;
public void set(int pX, int pY1, int pY2, int pSgn, int pId) {
x = pX;
y1 = pY1;
y2 = pY2;
sgn = pSgn;
id = pId;
}
public ToProcess() {
}
}
public static class ToProcessCompareAsc implements Comparator<ToProcess> {
@Override
public int compare(ToProcess o1, ToProcess o2) {
return o1.x - o2.x;
}
}
public static class ToProcessCompareDesc implements Comparator<ToProcess> {
@Override
public int compare(ToProcess o1, ToProcess o2) {
return o2.x - o1.x;
}
}
static int n, q;
static int[] p;
static ToProcess[] queryL, queryR;
static int queryLCnt, queryRCnt;
static SQRTDecomposition sum;
static ToProcessCompareAsc ascCmp = new ToProcessCompareAsc();
static ToProcessCompareDesc descCmp = new ToProcessCompareDesc();
public static final void add(int q, int sgn, int id) {
if (q-1 >= 0) {
queryL[queryLCnt++].set(q-1, p[q]+1, n-1, sgn, id);
}
if (q+1 < n) {
queryR[queryRCnt++].set(q+1, 0, p[q]-1, sgn, id);
}
}
public static void main(String[] args) throws Exception {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer tokenizer = new StringTokenizer(reader.readLine());
n = Integer.parseInt(tokenizer.nextToken());
q = Integer.parseInt(tokenizer.nextToken());
int[] qL = new int[q], qR = new int[q];
long[] ans = new long[q], preAns = new long[q];
p = new int[n];
for (int i = 0; i < n; i++) {
p[i] = i;
}
for (int i = 0; i < q; i++) {
tokenizer = new StringTokenizer(reader.readLine());
qL[i] = Integer.parseInt(tokenizer.nextToken()) - 1;
qR[i] = Integer.parseInt(tokenizer.nextToken()) - 1;
}
long cnt = 0;
boolean[] good = new boolean[n];
int[] goods = new int[n];
int goodsSize = 0;
queryL = new ToProcess[4 * BLOCK_SZ_Q]; queryR = new ToProcess[4 * BLOCK_SZ_Q];
for (int j = 0; j < 4 * BLOCK_SZ_Q; j++) {
queryL[j] = new ToProcess();
queryR[j] = new ToProcess();
}
SQRTDecomposition sum = new SQRTDecomposition(n, BLOCK_SZ_N);
for (int i = 0; i < q; i += BLOCK_SZ_Q) {
int iEnd = Math.min(q, i + BLOCK_SZ_Q);
Arrays.fill(good, false);
for (int j = i; j < iEnd; j++) {
good[qL[j]] = true;
good[qR[j]] = true;
}
goodsSize = 0;
for (int j = 0; j < n; j++) {
if (good[j]) {
goods[goodsSize++] = j;
}
}
long goodCnt = 0;
queryLCnt = 0;
queryRCnt = 0;
for (int j = i; j < iEnd; j++) {
int a = qL[j], b = qR[j];
if (a == b) {
ans[j] += goodCnt;
continue;
}
for (int k = 0; k < goodsSize; k++) {
int q = goods[k];
if (q == a || q == b) {
continue;
}
if ((p[q] < p[a] && q > a) ||
(p[q] > p[a] && q < a)) {
goodCnt--;
}
if ((p[q] < p[b] && q > b) ||
(p[q] > p[b] && q < b)) {
goodCnt--;
}
if ((p[q] < p[b] && q > a) ||
(p[q] > p[b] && q < a)) {
goodCnt++;
}
if ((p[q] < p[a] && q > b) ||
(p[q] > p[a] && q < b)) {
goodCnt++;
}
}
if ((a < b && p[a] > p[b]) ||
(a > b && p[a] < p[b])) {
goodCnt--;
} else {
goodCnt++;
}
ans[j] += goodCnt;
add(a, -1, j);
add(b, -1, j);
int tmp = p[a];
p[a] = p[b];
p[b] = tmp;
add(a, +1, j);
add(b, +1, j);
}
sum.clear();
Arrays.sort(queryL, 0, queryLCnt, ascCmp);
int curL = 0;
for (int j = 0; j < n; j++) {
if (!good[j]) {
sum.add(p[j], 1);
}
for (; curL < queryLCnt; curL++) {
ToProcess cur = queryL[curL];
if (cur.x != j) {
break;
}
int res = sum.sum(cur.y1, cur.y2);
res *= cur.sgn;
preAns[cur.id] += res;
}
}
sum.clear();
Arrays.sort(queryR, 0, queryRCnt, descCmp);
int curR = 0;
for (int j = n-1; j >= 0; j--) {
if (!good[j]) {
sum.add(p[j], 1);
}
for (; curR < queryRCnt; curR++) {
ToProcess cur = queryR[curR];
if (cur.x != j) {
break;
}
int res = sum.sum(cur.y1, cur.y2);
res *= cur.sgn;
preAns[cur.id] += res;
}
}
for (int j = i; j < iEnd; j++) {
if (j != i) {
preAns[j] += preAns[j-1];
}
ans[j] += cnt + preAns[j];
}
cnt = ans[iEnd - 1];
}
for (int i = 0; i < q; i++) {
writer.write(Long.toString(ans[i]));
writer.newLine();
}
reader.close();
writer.close();
}
}
class SQRTDecomposition {
private int n;
private int sz;
private int[] val;
private int[] blocks;
public final void add(int v, int delta) {
val[v] += delta;
blocks[v / sz] += delta;
}
public final int sum(int l, int r) {
if (l < 0) {
l = 0;
}
if (r >= n) {
r = n;
}
r++;
int res = 0;
int lBlock = (l + sz - 1) / sz, rBlock = r / sz;
for (int i = lBlock; i < rBlock; i++) {
res += blocks[i];
}
int lBlockR = lBlock * sz, rBlockR = rBlock * sz;
if (lBlockR >= rBlockR) {
for (int i = l; i < r; i++) {
res += val[i];
}
} else {
for (int i = l; i < lBlockR; i++) {
res += val[i];
}
for (int i = rBlockR; i < r; i++) {
res += val[i];
}
}
return res;
}
public void clear() {
Arrays.fill(val, 0);
Arrays.fill(blocks, 0);
}
SQRTDecomposition(int pN, int pSz) {
n = pN;
sz = pSz;
val = new int[n];
blocks = new int[(n + sz - 1) / sz];
}
}
Alternative solution from Vladik:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <set>
#include <map>
#include <vector>
#include <iomanip>
#define sqr(a) (a)*(a)
#define all(a) (a).begin(), (a).end()
using namespace std;
template <typename T>
T next_int() {
T ans = 0, t = 1;
char ch;
do { ch = getchar(); } while(ch <= ' ') ;
if(ch == '-') {
t = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9') {
ans = ans * 10 + (ch - '0');
ch = getchar();
}
return ans * t;
}
string next_token() {
char ch;
string ans = "";
do { ch = getchar(); } while(ch <= ' ') ;
while(ch >= ' ') {
ans += ch;
ch = getchar();
}
return ans;
}
const long long INF = (long long)1e18 + 227 + 1;
const int INFINT = (int)1e9 + 227 + 1;
const int MAXN = (int)2e5 + 227 + 1;
const int MOD = (int)1e9 + 7;
const long double EPS = 1e-9;
long long bin_pow(long long n, long long k) {
if(!k) return 1;
long long ans = bin_pow(n, k / 2);
ans = ans * ans % MOD;
if(k % 2) ans = ans * n % MOD;
return ans;
}
struct tree {
int size_block;
int len;
tree(int len) : len(len) {
size_block = sqrt(len);
kek.resize(len / size_block + 1, vector<int>(size_block, 0));
pr_block.resize(len / size_block + 1, 0);
}
vector<int> pr_block;
vector<vector<int> > kek;
void inc(int pos, int num) {
int x = pos / size_block;
for(int i = pos % size_block; i < size_block; i++) {
kek[x][i] += num;
}
for(int i = 0; i <= len / size_block; i++)
if(i == 0) {
pr_block[i] = kek[i][size_block - 1];
} else {
pr_block[i] = pr_block[i - 1] + kek[i][size_block - 1];
}
}
int f(int a) {
return a / size_block;
}
long long get(vector<int> &a, int l, int r, bool ok = 1) {
if(ok == 1) {
l %= size_block;
r %= size_block;
}
return a[r] - (l ? a[l - 1] : 0);
}
int get(int l, int r) {
if(l > r) return 0;
r = min(r, len);
if(f(l) == f(r))
return get(kek[f(l)], l, r);
int ans = 0;
if(l % size_block) {
ans += get(kek[f(l)], l, size_block - 1);
l += size_block - l % size_block;
}
if(r % size_block != size_block - 1) {
ans += get(kek[f(r)], 0, r);
r -= r % size_block + 1;
}
ans += get(pr_block, f(l), f(r), 0);
return ans;
}
int get_pref(int p) {
return get(1, p - 1);
}
int get_suff(int p) {
return get(p + 1, len);
}
} ;
struct mda {
vector<int> a;
vector<tree> t;
int len, sz;
long long ans;
mda(int len) : len(len) {
sz = 2000;
ans = 0;
a.resize(len + 1);
for(int i = 1; i <= len; i++)
a[i] = i;
for(int i = 1; i <= len; i += sz) {
t.push_back(tree(len));
for(int j = i; j < i + sz && j <= len; j++)
add(j, j);
}
}
int get_pref(int L, int R, int k) {
int ans = 0;
for(int l = 1; l <= R; l += sz) {
int r = l + sz - 1;
if(r < L || l > R) continue;
if(L <= l && r <= R)
ans += t[(l - 1) / sz].get_pref(k);
else
for(int i = max(l, L); i <= min(r, R); i++)
ans += (a[i] < k);
}
return ans;
}
int get_suff(int L, int R, int k) {
int ans = 0;
for(int l = 1; l <= R; l += sz) {
int r = l + sz - 1;
if(r < L || l > R) continue;
if(L <= l && r <= R)
ans += t[(l - 1) / sz].get_suff(k);
else
for(int i = max(l, L); i <= min(r, R); i++)
ans += (a[i] > k);
}
return ans;
}
void del(int p, int k) {
p = (p - 1) / sz;
t[p].inc(k, -1);
}
void add(int p, int k) {
p = (p - 1) / sz;
t[p].inc(k, 1);
}
void sw(int i, int j) {
if(i == j) return;
if(i > j) swap(i, j);
ans -= get_pref(i, j, a[i]);
ans -= get_suff(i, j, a[j]);
if(a[i] > a[j]) ans++;
del(i, a[i]);
del(j, a[j]);
swap(a[i], a[j]);
add(i, a[i]);
add(j, a[j]);
ans += get_pref(i, j, a[i]);
ans += get_suff(i, j, a[j]);
if(a[i] > a[j]) ans--;
}
} ;
int main() {
// freopen(".in", "r", stdin);
int n, m; cin >> n >> m;
mda t(n);
for(int i = 0; i < m; i++) {
int x, y; cin >> x >> y;
t.sw(x, y);
cout << t.ans << "\n";
}
}
Alternative solution from netman:
import java.io.*;
import java.util.*;
public class NsqrtNlogNnetman implements Runnable {
static class InputReader {
BufferedReader reader;
StringTokenizer tokenizer;
InputReader(InputStream in) {
reader = new BufferedReader(new InputStreamReader(in), 32768);
tokenizer = null;
}
String next() {
while (tokenizer == null || !tokenizer.hasMoreTokens()) {
try {
tokenizer = new StringTokenizer(reader.readLine());
} catch (IOException e) {
e.printStackTrace();
throw new RuntimeException(e);
}
}
return tokenizer.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
long nextLong() {
return Long.parseLong(next());
}
double nextDouble() {
return Double.parseDouble(next());
}
}
static class Fenwick {
int[] ft;
Fenwick(int n) {
ft = new int[n];
}
void add(int r, int val) {
while (r < ft.length) {
ft[r] += val;
r |= r + 1;
}
}
int sum(int r) {
int res = 0;
while (r >= 0) {
res += ft[r];
r = (r & (r + 1)) - 1;
}
return res;
}
void clear() {
Arrays.fill(ft, 0);
}
}
static class Query {
int x, bound, sign, id;
Query(int x, int bound, int sign, int id) {
this.x = x;
this.bound = bound;
this.sign = sign;
this.id = id;
}
}
static void getOnPrefSmaller(List<Query> qrs, int r, int y, int id, int sign) {
qrs.add(new Query(r, y, sign, id));
}
static void getOnPrefBetween(List<Query> qrs, int r, int x, int y, int id, int sign) {
getOnPrefSmaller(qrs, r, y, id, sign);
getOnPrefSmaller(qrs, r, x, id, -sign);
}
static void getOnSegmentBetween(List<Query> qrs, int l, int r, int x, int y, int id, int sign) {
if (x > y) return;
getOnPrefBetween(qrs, r, x, y, id, sign);
getOnPrefBetween(qrs, l, x, y, id, -sign);
}
@Override
public void run() {
InputReader in = new InputReader(System.in);
PrintWriter out = new PrintWriter(System.out);
int n = in.nextInt();
int q = in.nextInt();
int[] l = new int[q];
int[] r = new int[q];
for (int i = 0; i < q; i++) {
l[i] = in.nextInt() - 1;
r[i] = in.nextInt() - 1;
}
int[] perm = new int[n];
for (int i = 0; i < n; i++) {
perm[i] = n - i - 1;
}
final int BLOCK = 300;
long inv = 0L;
boolean[] isInteresting = new boolean[n];
long[] add = new long[q];
Fenwick f = new Fenwick(n);
for (int i = 0; i < q; i += BLOCK) {
int from = i, to = Math.min(i + BLOCK, q) - 1;
List<Integer> lst = new ArrayList<>();
for (int j = from; j <= to; j++) {
lst.add(l[j]);
lst.add(r[j]);
}
lst.sort(Integer::compareTo);
lst = new ArrayList<>(new HashSet<>(lst));
int[] interestingPositions = lst.stream().mapToInt(x -> x).toArray();
for (int pos : interestingPositions) {
isInteresting[pos] = true;
}
List<Query> qrs = new ArrayList<>();
for (int j = from; j <= to; j++) {
if (l[j] == r[j]) continue;
if (l[j] > r[j]) {
int tmp = l[j];
l[j] = r[j];
r[j] = tmp;
}
if (perm[l[j]] < perm[r[j]]) {
getOnSegmentBetween(qrs, l[j], r[j], perm[l[j]], perm[r[j]], j,-1);
int leftValue = perm[l[j]];
int rightValue = perm[r[j]];
for (int pos : interestingPositions) {
if (pos > l[j] && pos < r[j] && perm[pos] > leftValue && perm[pos] < rightValue) {
add[j] -= 2;
}
}
add[j]--;
} else {
getOnSegmentBetween(qrs, l[j], r[j], perm[r[j]], perm[l[j]], j,1);
int leftValue = perm[l[j]];
int rightValue = perm[r[j]];
for (int pos : interestingPositions) {
if (pos > l[j] && pos < r[j] && perm[pos] > rightValue && perm[pos] < leftValue) {
add[j] += 2;
}
}
add[j]++;
}
int tmp = perm[l[j]];
perm[l[j]] = perm[r[j]];
perm[r[j]] = tmp;
}
qrs.sort(Comparator.comparingInt(a -> -a.x));
f.clear();
for (int pos = 0; pos < n; pos++) {
if (!isInteresting[pos]) {
f.add(perm[pos], 1);
}
while (!qrs.isEmpty() && qrs.get(qrs.size() - 1).x == pos) {
Query t = qrs.get(qrs.size() - 1);
qrs.remove(qrs.size() - 1);
add[t.id] += 2 * t.sign * f.sum(t.bound);
}
}
for (int j = from; j <= to; j++) {
inv += add[j];
out.println(inv);
}
for (int pos : interestingPositions) {
isInteresting[pos] = false;
}
}
out.close();
}
public static void main(String[] args) {
new Thread(null, new NsqrtNlogNnetman(), "1", 1L << 28).run();
}
}







