Hello Codeforces Community!
I have been solving some interesting bitmasks problems. In some problems, we have to generate all possible subsets from a set. Obviously, if our set is a bitmask with all its bits on, we can iterate from 0 to 2n - 1
However, if we need to generate all the subsets from another subset (subset-ception), we can do it with the following procedure:
for(subset = set; subset > 0; subset = (subset - 1)&set)
(The code above ignores the empty subset)
Generate all the subsets from all possible subsets has O(3n) complexity. Now, I can intuitively confirm this, because we can represent our subsets as a string with 3 possible values: while 1 and 0 at position i means that the object i is in our subset or not respectively, 2 means that the object i is not present in the set at all.
However, mathematically:
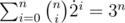
Amazing! I cannot find a way to prove this though. Do you know how to prove this interesting property?





