I'm trying to find efficient algorithm for finding shortest path in weighted(Positive/Negative) graph with maximum edge limit.

For example, in the graph below if we demand the shortest path from A to C with restriction the path can contain at most two edges. It would be A->B->C and total cost 5 (Which is greater than A->D->E->C)

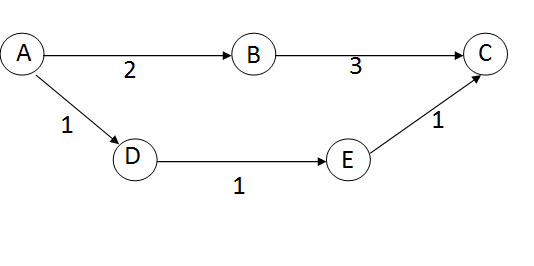
I think when the graph is (directed or undirected) has no negative edge, we can use Dijkstra with little modification, such that we will keep the number of edges in the currently discovered shortest path from source to currently used vertex for relaxation. Is my idea OK? Or there is much better something?

And how can we solve the similar problem when the graph(directed) consists of negative edges(but no negative cycle)?