On the e-maxx website about the Disjoint Set Union data structure there is a paragraph about computing range minimum queries offline using DSU. (http://e-maxx.ru/algo/dsu#15)

It is claimed that it works in O(α(n)) time per query on average (α is the inverse Ackerman function).

My Russian is terrible, and Google/Yandex translate also is quite hard to understand for this paragraph. So I have some questions about this one.

From what I can understand using Google translate is the following:

• this only works if the elements are actually a permutation of 1 to n (otherwise we would have to sort the elements beforehand)
• for each index in the array we store the reference to the closest query that ends right of the index.

From this information I was able to construct this tree/forest structure. (red are the range queries, blue arrows are the references that point to the parent)

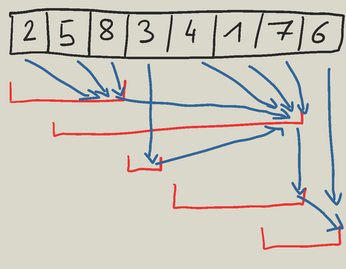
Now the algorithm then goes as follows:

• We start with the empty array.
• We insert the smallest number 1 and follow the references. In that way we visit all range queries where 1 is the answer. Therefore we can answer those, and shorten some of the paths via path compression and Union by rank (the typical DSU optimizations).
• The repeat the procedure with the other elements in increasing order.

I'm pretty sure I know how to create the data structure in linear time [first store every query (left, right) at left, then do walk through it and store the queries at right (this assures that multiple queries that end in the same element are sorted by size in descending order, Then iterate over those in reversed order keeping a stack with the current biggest/active queries.]

So everything looks quite lovely and fine.

But now I have one main concern.

I'm pretty sure that I can create test cases in which a query takes O(n) time on average. E.g. take the sorted array 1, 2, 3, ..., n, and taking n/3 queries of the type [1, 2n/3], [2, 2n/3], [3, 2n/3], ..., and the add n/3 queries of the type [n/3, 2n/3], [n/3+1, 2n/3+1], [n/3+2, 2n/3] ... For each inserted element we would have to iterate over all n/3 queries of the second type to be sure that none of these has the current element as answer. Because theoretically they could all start at the index 1 of the array.

So my question: Have I completely misunderstood what the Russian explanation says? Do I have to structure the DSU differently? Or is the explanations wrong and doing RMQ with a DSU in that time actually impossible?