Hi Codeforces community! I wanted to write this blog entry to help coders who would like to see a nice example of convolutions used in a problem which, at first sight, has little to no relation with polynomial multiplication (of course it has, it's a convolution after all)
The problem is as follows: You are given two strings S and P, with lengths n and m respectively, where m ≤ n
For each substring T of S with length m, we have to find the one that maximizes the number of positions with the same character, i. e T[i] = P[i]
For the sake of simplicity, let us assume that our strings consists only of letters a and b. For example, if S = baabab and P = bba, let's calculate the "similarity" between P and each substring of S of length 3.
s(baa, bba) = 2
s(aab, bba) = a
s(aba, bba) = 2
s(bab, bba) = b
We can see that there are two substrings which maximize the similarity (any answer will be fine)
A naive approach has a O(n·m) time complexity and uses O(n + m) memory.
This should be OK if 1 ≤ n, m ≤ 1000. What about 1 ≤ n, m ≤ 105? We have to find a faster way to apply  for every substring T of S
for every substring T of S
First, let's try to change the formula above with a more mathematical approach. If we map each character {a,b}={0,1}, we can apply the next formula:
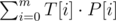 . This will give us the number of 1's (originally, b's) that match.
. This will give us the number of 1's (originally, b's) that match.
Let Sc be the complement of S (0 becomes 1, and viceversa). To compute the number of 0's that match, we apply
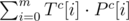
Now what? This doesn't improve the complexity at all.
Let's remember how the convolution f of two discrete functions g and h is defined:
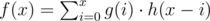
Now we're talking! This looks pretty similar to the formulas previously explained.
Next we will try to change our formulas to a simple convolution. First we will say that our array S and P are two functions g and h whose domain is [0, n - 1] and range is {0,1}.
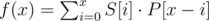
We have one issue to address, the length of P (m). We can easily fix this issue with adding some padding zerores to the right of P until m = n
But the formula is incorrect, this convolution, for each x applies the similarity formula, but reversing P! This is our second issue, which we can easily solve (again) by reversing P ourselves





