I am reading the article on this website https://www.cs.colorado.edu/~srirams/courses/csci2824-spr14/pollardsRho.html to understand Pollard rho factorization.
I will explain my doubt with an example.
Suppose for N = p * q, we have 35 = 5 * 7 where N = 35,p = 5,q = 7.
Probability of finding factor 5 from [1...35] is 1 / 35.
To increase the probability of getting the factor 5, we search for number x such that GCD(x, N) = 5. Numbers 5, 10, 15, 20, 25, 30 satisfy the equation GCD(x, N) = 5. So probability of finding factor 5 increases to 6 / 35.
Now they have mentioned that to increase the probability further, we find pairs of numbers such that |Xi - Xj| = Yi where Yi is 5, 10, 15, 20, 25, 30.
Number of pairs satisfying the criteria |Xi - Xj| = 5 is 30 * 2 = 60, similarly number of pairs satisfying |Xi - Xj| = 10 is 25 * 2 = 50 and so on..
So to get factor 5, we need to search (30 + 25 + 20 + 15 + 10 + 5) * 2 pairs out of 35 * 35 pairs. So the probability of getting required pair is (210) / (35 * 35) = 6 / 35 which is same as the one where we found factor 5 using GCD(x, N) without searching for pairs.
So my doubt is, to find required factor, why do we search for 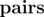 such that GCD(|Xi - Xj|, N) = p instead of GCD(Xi, N) = p as their probabilities are same ?
such that GCD(|Xi - Xj|, N) = p instead of GCD(Xi, N) = p as their probabilities are same ?





