Прошу подтвердить либо опровергнуть мои нижеследующие утверждения о теории позиционных игр. Ссылки на источники, где это объяснено, тоже приветствуются. Но именно источники, где объяснена взаимосвязь или показана её невозможность (либо веские причины для сомнительности), а не просто отдельный источник о чём-то одном и отдельный о чём-то другом.

Мои утверждения коротко:

1. Свед_е_ние пристрастных игр к беспристрастным возможно всегда, пока ограничиваемся выигрышностью / проигрышностью позиций, но не используем ту теорему Шпрага-Гранди, которая позволяет ксорить SG игр и узнавать SG их суммы. Если используем -- использовать свед_е_ние нельзя, и исключений то ли вообще нет, то ли они какие-то очень-очень узкие и странные.

2. Хотя существует алгоритм решения "мизерного Нима", или "Нима в поддавки", в подавляющем большинстве случаев его нельзя обобщить на другие игры тем же способом, которым тому, как обычный Ним обобщается на все игры, решаемые через SG.

Более подробная версия -- под катом. Игра называется пристрастной, если перечень возможных ходов из одной и той же позиции может (хотя бы иногда) зависеть от того, кто из игроков ходит. Если таких зависимостей нет, игра беспристрастная.

В некоторых ситуациях, пристрастная игра может быть искусственно сведена к "как бы беспристрастной" путём того, что позиция включает в себя также и информацию о том, кто сейчас ходит. После такого уточнения понятия "позиция", ход начинает определяться только позицией. Если игра конечна, ациклична, завершается выигрышем одного игрока и проигрышем другого, и эти выигрыш&проигрыш не имеют числового или ещё какого-то выражения, а просто выигрыш/проигрыш -- вполне можно, например, расставить каждой позиции её выигрышность/проигрышность, действуя по обычным правилам "позиция проигрышна, если тот, кому она досталась, этим уже проиграл, или все допустимые ходы ведут в выигрышные позиции; позиция выигрышна, если тот, кому она досталась, этим уже выиграл, или есть хотя бы один допустимый ход, ведущий в проигрышную позицию". И тут пристрастность начальной формулировки игры никак всему этому не мешает, лишь бы было правильно проведено преобразование позиций и ходов. Причём, тут НЕТУ требования "проигрывает тот, кто не может походить" -- можно рассматривать хоть игры, в которых тот, кто не может походить, проигрывает, хоть игры, в которых тот, кто не может походить, выигрывает, хоть игры, в которых часть позиций, из которых нельзя походить, проигрышна, а часть выигрышна (лишь бы это чётко описывалось правилами игры).

Если функция Шпрага-Гранди формально вроде бы и используется, но особенности игры таковы, что фактически используется один только mex без ксора, то добавляется ограничение, что всё это справедливо только для игр, в которых тот, кому некуда ходить, проигрывает. Однако возможность сведения пристрастных игр к беспристрастным остаётся. С другой стороны, непонятно, чем такое использование Шпрага-Гранди вообще лучше одних только выигрышных/проигрышных позиций.

А в ситуации, когда функция Шпрага-Гранди используется полноценно, включая свойство "SG суммы игр равно ксору SG этих игр" -- вот тогда сводить пристрастные игры к беспристрастным нельзя. По крайней мере, нельзя вышеупомянутым способом, и не существует никакого известного другого. И нельзя потому, что когда происходит разбиение позиции на несколько независимых (SG которых ксорятся), теряется свойство "просто введём в позицию, кто ходит, и каждый игрок автоматически будет получать только те позиции, из которых ходит именно он".

Например, рассмотрим такую игру. Есть полоска, вначале состоящая из N клеточек, расположенных одной непрерывной последовательностью. Алиса может на каждом своём ходу вычеркнуть любые идущие подряд 2, или 4, или 16 клеточек. Боб может вычеркнуть на каждом своём ходу любые идущие подряд 1, или 2, или 3 клеточек. Проигрывает, по-стандартному, тот, кому некуда ходить.

Пусть начальная позиция "ходит Алиса, один непрерывный кусок из 8 клеточек", что в терминах, использующих сумму игр и ксор результатов SG, было бы удобно обозначать как "(Алиса, 8)", а в терминах, не использующих сумму игр, например, как "(Алиса, 00000000)", где "0" -- чистая(целая), "1" -- "зачёркнутая". Среди ходов Алисы есть ход "разорвать полоску двумя клеточками, вычеркнутыми ровно посредине", т.е. перейти в позицию "(Боб, 00011000)". При переходе к сумме игр и ксору результатов SG должно быть сказано, что получается сумма двух игр "(Боб, 3)", и даже не важно, чему конкретно равно SG((Боб, 3)), всё равно ксор двух одинаковых чисел даст ноль, что будто бы доказывает, что такой ход Алисы приносит ей выигрыш. Однако, рассмотрев всё это без ксора SG, видим, что Боб из позиции (Боб, 00011000) может пойти в позицию (Алиса, 11111000), зачеркнув все три клеточки первой из "половин". Когда Алисе достаётся позиция (Алиса, 11111000), она может пойти ТОЛЬКО или в (Боб, 11111110), или в (Боб, 11111011), и после любого из этих ходов Боб зачёркивает одну последнюю клеточку и выигрывает.

Я не провёл анализ, может ли Алиса обеспечить себе выигрыш каким-то другим первым ходом; но ведь смысл всего этого примера -- показать, почему настолько просто совмещать сведение пристрастных игр к беспристрастным с теоремой Шпрага-Гранди вроде как не получается.

=======================================

Во многих местах, включая страницу "Функция Шпрага — Гранди" википедии говорится, что "Функция Шпрага-Гранди определяется для игр с двумя игроками, в которых проигрывает игрок, не имеющий возможности сделать очередной ход".

На e-maxx (страница "Теория Шпрага-Гранди. Ним", пункт "Ним в поддавки") утверждается: "... существует также "ним в поддавки" ("misère nim") — когда игрок, совершивший последний ход, проигрывает (а не выигрывает) ... Решение такого нима удивительно просто: будем действовать так же, как и в обычном ниме (т.е. посчитаем XOR-сумму всех размеров кучек, и если она равна нулю, то мы проиграем при любой стратегии, а иначе — выиграем, найдя переход в позицию с нулевым значением Шпрага-Гранди). Но есть одно исключение: если размеры всех кучек равны единице, то выигрышность/проигрышность меняются местами по сравнению с обычным нимом."

Например, единственная игра g₁ с SG(g₁) = 1 вполне может распасться в сумму двух игр g₁₁, g₁₂, таких, что SG(g₁₁) = SG(g₁₂) = 2 ? Получаем, что 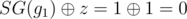, (где определение z см. на всё той же странице e-maxx), и получается ход из проигрышной в проигрышную, что полностью противоречит определению выигрышности/проигрышности и взаимосвязи между SG и выигрышностью/проигрышностью.

=======================================

Повторяю: всё это писано не как тьюториал, а как изложение того, как я на текущий момент понимаю взаимосвязь, допускаю возможность ошибок в своём понимании, и прошу указать на них, если они есть.