Не хотел создавать данный пост — надеялся, что кто-то другой сделает, но нет :) На этой неделе проходят областные олимпиады в Беларуси. Все как обычно, два тура по 4 задачи, 5 часов на их решение. Здесь предлагаю обсудить задачки, решения и так далее.
Первый тур
Задача 1. Олимп-Сити
Сложность по времени 
Задача 2. Дружелюбные соседи
Решим задачу для полоски. А решать такую задачу можно жадно. Ведь действительно, если мы можем поставить очередную перегородку в позициях i и i + 1, то будет не хуже, если мы поставим в i + 1. Чтобы понять, нужно ли нам ставить перегородку, будем хранить текущий OR чисел, между которыми еще нет перегородок. Если AND с очередным числом дает больше 1, то мы обязаны поставить перед этим числом перегородку.
Чтобы решить исходную задачу, нужно перебрать позицию первой перегородки. После этого, задача сводится к задаче на полоске. К сожалению, такое решение работает за квадрат, что недостаточно быстро. Но заметим забавный факт — расстояние между перегородками не будет превышать 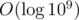 . Поэтому нам достаточно перебрать первые
. Поэтому нам достаточно перебрать первые 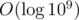 позиций для первой перегородки.
позиций для первой перегородки.
Сложность по времени:  , по памяти: O(n).
, по памяти: O(n).
Задача 3. Поворот плиток
Нужно рассмотреть много случаев. Для школьников это не должно быть проблемой, ведь у каждого собственная тетрадка для записей :) Не бойтесь, случаев не так уж и много, а при написании решения они вообще не будут использоваться (только следствие из них).
Рассмотрим плиточку. Если плиточка пустая, то ничего интересного не произойдет, так как поворот ни на что не влияет. Поэтому посмотрим на непустую плитку. Тут на самом деле все просто. В этой плитке могли встретится:
- Цикл и цикл — тогда поворот такой плитки уменьшает количество циклов на 1;
- Цикл и цепочка — тогда поворот опять уменьшает количество циклов на 1, количество цепочек остается прежним;
- Цепочка и цепочка — поворот никак не повлиял на количество циклов и цепочек;
Задача 4. Садовник
Дан массив a из n чисел и q запросов. Запросы двух типов:
- 1 x — увеличить все числа x в массиве a на 1.
- 2 l r z — посчитать, сколько чисел на отрезке от l до r не больше z.
Научимся отвечать на запросы без модификаций массива. Для начала положим, что zi не убывают. Будем хранить новый массив t. Для i-го запроса, он будет выглядеть так:
ti = 0, если ai > zi,
ti = 1, если ai ≤ zi.
Как переходит от i-го массива к i + 1 понятно — нужно в нужных местах добавить 1. Чтобы отвечать на запрос от l до r, нам необходимо посчитать сумму на отрезке в массиве t. Чтобы делать это быстро, будем хранить t как дерево отрезков.
Теперь избавимся от ограничения на zi. Для этого сделаем наше дерево отрезков персистентным. Большему zi должна соответствовать большая версия, поэтому чтобы построить такое дерево отрезков, отсортируем исходный массив ai и занесем в персистентное дерево отрезков. Для всех возможных значений zi запомним максимальный номер версии, запрос к которой будет соответсвовать запросу li, ri, zi. Будем хранить номер в массиве v. Отвечать на запросы мы научились.
Теперь посмотрим, что происходит, когда мы делаем операцию инкремента чисел равных x. Если до инкремента запросу l, r, x соответсвовал запрос в дереве отрезков с версией v[x], то после инкремента ответ можно получить в v[x - 1]. Для чисел не равных x не поменялось ничего. Поэтому, чтобы выполнить операцию инкремента, нам необходимо сделать v[x] = v[x - 1].
Сложность по времени: 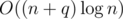 , по памяти:
, по памяти: 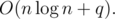
Второй тур
Задача 1. Доставка почты
Задача 2. Контрольная работа
Найдем все делители di числа m. Посчитаем fi — количество чисел 1 ≤ j ≤ k таких, что gcd(m, j) = d[i]. По факту, мы уже умеем решать задачу при n = 1. Как получить ответ для n > 1? Давайте поймем, как получать ответ для n = 2. Пусть px — этотакоечисло, чтоd[p[x]] = x. Посчитаем gk как сумму fi·fj таких, что gcd(m, di·dj) = dk. Собственно мы получили массив f, но для n = 2 путем слияния двух ответов для n = 1. Как получить ответ для n = 3? Сольем ответы для n = 2 и n = 1 (то есть f и g). Такое слияние мы делаем за 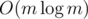 , но если предподсчитать gcd за
, но если предподсчитать gcd за 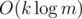 , то слияние можно делать за O(m). Собственно мы получили решение за
, то слияние можно делать за O(m). Собственно мы получили решение за 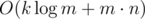 . Заметим, что слияние можем делать сразу степенями двойки, но ограничения задачи не требовали этого.
. Заметим, что слияние можем делать сразу степенями двойки, но ограничения задачи не требовали этого.
Сложность по времени: 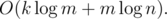
Задача 3. Текстовый редактор
Задача 4. Послание инопланетянам
Во первых, избавимся от строк, которые полностью входят в другие строки. Теперь посчитаем такую метрику d(i, j) — минимальная длина строки, префикс которой является строкой si, а суффикс sj. Теперь представим каждую строку как вершину графа, а ребра как склеивания этих строк. Наша задача найти кратчайший путь, такой, что все вершины мы посетим один раз. Другими словами найдем гамильтонов путь в графе. А потом просто его восстановим. Вершин всего 30, поэтому придется немного подождать, так как потребуется порядка 2^30*30 операций.
Для данных тестов можно поступить еще проще — выбирать ребра жадно.





