Because 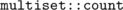works in O(n) time.

Quite recently I needed to solve this kind of problem:

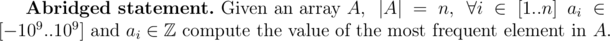
I decided to use , since it had some useful method called . And since I needed to count the elements I coded something like this:

int main() {
    int n;
    vector<int> a(n);
    multiset<int> cnt;

    /* Read array */

    // Insert elements in multiset
    for (auto i : a)
        cnt.insert(i);
    
    // Choose among all elements of a the most frequent
    int ans = 0;
    for (auto &i : cnt)
        ans = max(ans, cnt.count(i));
    
    cout << ans << endl;

    return 0;
}

Now. The problem was that this code was judged TLE for, seemingly, no reason at all! Having lost thirty minutes trying to understand where my complexity analysis skills failed, in desperation, I replaced multiset with an ordinary map:

int main() {
    int n;
    vector<int> a(n);
    map<int, int> cnt;

    /* Read array */

    // Insert elements in multiset
    for (auto i : a)
        cnt[i]++;
    
    // Choose among all elements of a the most frequent
    int ans = 0;
    for (auto &i : cnt)
        ans = max(ans, cnt[i]);
    
    cout << ans << endl;

    return 0;
}

and it passed! But I was still a bit salty, so I tried to figure out why did this happen: clearly there is something wrong with multiset.

First of all, insertion and searching in multiset and map is the same 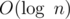since they both internally implemented as Red-Black trees. The only thing that is nor the first nor the latter is the count method in the first snippet. So, it must be the reason why it failed.

At this point, I've dived into the source code of the libc++. The headers for it on Unix machine should be located at /usr/include/c++//, where is the version of the compiler (run g++ -v to get it). There we can see vector algorithms and (needed me now) set files among many. cat set yieldes

// Licence is omitted

/** @file include/set
 *  This is a Standard C++ Library header.
 */

#ifndef _GLIBCXX_SET
#define _GLIBCXX_SET 1

#pragma GCC system_header

#include <bits/stl_tree.h>
#include <bits/stl_set.h>
#include <bits/stl_multiset.h>
#include <bits/range_access.h>

#ifdef _GLIBCXX_DEBUG
# include <debug/set>
#endif

#ifdef _GLIBCXX_PROFILE
# include <profile/set>
#endif

#endif /* _GLIBCXX_SET */

It's just a bunch #include derivatives of other low level files! I'm interested in multiset, so it will be logical to visit stl_multiset.h and look at the count method:

      size_type
      count(const key_type& __x) const
      { return _M_t.count(__x); }

which just delegates the task to the _M_t field that is defined at the beginning of the class as

      /// The actual tree structure.
      _Rep_type _M_t;

and _Rep_type as a typedef for

      /// This turns a red-black tree into a [multi]set.
      typedef typename __gnu_cxx::__alloc_traits<_Alloc>::template
	rebind<_Key>::other _Key_alloc_type;

      typedef _Rb_tree<key_type, value_type, _Identity<value_type>,
		       key_compare, _Key_alloc_type> _Rep_type;

Red-Black tree. Its definition is contained within std_tree.h with a sought method count:

  template<typename _Key, typename _Val, typename _KeyOfValue,
	   typename _Compare, typename _Alloc>
    typename _Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::size_type
    _Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::
    count(const _Key& __k) const
    {
      pair<const_iterator, const_iterator> __p = equal_range(__k);
      const size_type __n = std::distance(__p.first, __p.second);
      return __n;
    }

Ignoring all these scary looking templates, we can see that the count method is just three lines long! Namely, in the first line we get a pair of two iterators, first of which points to the first element with its key equal to __k in the set and the second -- to the last. In the second line we use std::distance to count elements between the first and the last element __p points to. Since _Rb_tree is a balanced binary search tree, we know that if we commit a DFS descent (обход) and write out the nodes in order of traversal, we get a sorted sequence. What std::distance does is just consequently iterates from __p.first forward and onward until reaches __p.second. Since we know that between them are the nodes with the same key, this counting will yield us the answer.

So... std::distance has linear time complexity! It jumps between different locations of memory step-by-step until reaching the terminal node. Basically, there's no other way to count nodes within the tree (Althought, I know that you can (somehow) invoke custom instance of gcc's tree that will be able to accompany each node with a subtree's size field, which can be used to bring down the complexity of .count up to 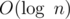but I need clarification on this).

The only difference between set and multiset is that multiset does not depend on the uniqueness of the nodes. Look at these two excerpts:

      // Set's insert
      std::pair<iterator, bool>
      insert(const value_type& __x)
      {
	std::pair<typename _Rep_type::iterator, bool> __p =
	  _M_t._M_insert_unique(__x);
	return std::pair<iterator, bool>(__p.first, __p.second);
      }

and

      // Multiset's insert
      iterator
      insert(const value_type& __x)
      { return _M_t._M_insert_equal(__x); }

The (almost) only difference is that that set uses ._M_insert_unique and multiset ._M_insert_equal that doesn't care about uniqueness: it will just put there another node with the same key.

And... reflecting on this, if we had an array full of ones, for example, to .count ones with a multiset we would need around O(n) time, thus dramastically degrading the overall complexity of the algorithm to O(n²)!

I don't know if I need to outline the moral of the story or not... Well, I guess, it's pretty straightforward, don't count with multisets.