Recently, I was asked to help flesh out a problem for the NAIPC 2019 contest whose problems are also used every year as the "Grand Prix of America". I helped write a solution and create some of the test data for this problem. The problem was called Cost Of Living
From the problem setter's perspective, this was intended to be an easy, A-level problem: suppose you have an table of values ay, c that meet the condition that:  for some mc > 0.
for some mc > 0.
If you are given a subset of the values in this table, and a subset of the values for ik, determine whether a set of queried values ay', c' is uniquely determined or not. Note that a0, c = bc.
Most contestants immediately realized that above product can be written as a sum by taking the logarithm:
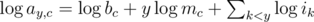
Each given value thus represents a linear equation in unknowns 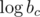 ,
, 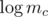 , and
, and 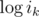 (plus some trivial equations for the subset of ik that may be given. On the right hand side of the system appear the logarithms of the given table values. The left hand side of the system has only integer coefficients. Each row contains y + 1 1's and one coefficient with value y.
(plus some trivial equations for the subset of ik that may be given. On the right hand side of the system appear the logarithms of the given table values. The left hand side of the system has only integer coefficients. Each row contains y + 1 1's and one coefficient with value y.
Each query, in turn, can also be written as a linear equation by introducing a variable 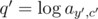 :
:
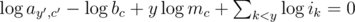
Now, all that is left is to solve for the query variables using a traditional method (Gaussian Elimination with partial pivoting) and report the results — or so we thought.
However, there was a great deal of uncertainty among some contestants whether this approach would work. One team attempted to solve the problem with a homegrown variant of Gaussian elimination, but got WA because their answer was too far off the requested answer (the answer had to be given with 1e-4 rel tolerance in this problem).
When they downloaded the judge data scripts, they observed that the amount of error in their implementation changed when they printed the input data with higher precision, which was very confusing to them.
For this problem, the input data was not given with full precision because it involves products with up to 20 factors. For instance, if bc = mc = ik = 1.1 than a10, c = 6.72749994932560009201 (exactly) but the input data would be rounded to 6.7274999493. If they changed this and printed instead 6.72749994932561090621, their solution would be much closer to the expected answer. Their result become even better when they used a floating point number type that uses more bits internally, such as quad-precision floats or java.math.BigDecimal.
What could account for this phenomenon?
The answer lies in a property of numerical algorithm call stability. Stability means that an algorithm does not magnify errors (approximations) in the input data; instead, the error in the output can be bounded by some factor.






