Problem Link: https://codeforces.net/contest/1187/problem/E
I am writing this blog partly because i wanna rethink what the solution is and partly it may help someone. So we are given a graph and we need maximum points by choosing white vertices. Obvious greedy approach to this would be to take the root add points gained by it, then take the children (as this would give the maximum points greedily) and add their points to the contribution and so on. Now the problem is we can't tell which root will be giving us an optimal answer. Also according to the input size given we cant run dfs separately for each vertex. So thus we need an observation to reduce the time complexity so that we can get Accepted. Observation:
Re rooting the vertex of the graph to any of its children only changes few things and this is the main observation needed to solve this problem. Below i choose a graph :

here i will start by choosing 2 as my root. So consider how we can get the max points here. Points by root = N(all the nodes) + points by child 1 + points by child 6.
So we can use dp to get points of children and the answer becomes dp[2] = sz[2] + dp[1] + dp[6] (sz[2] = 9)
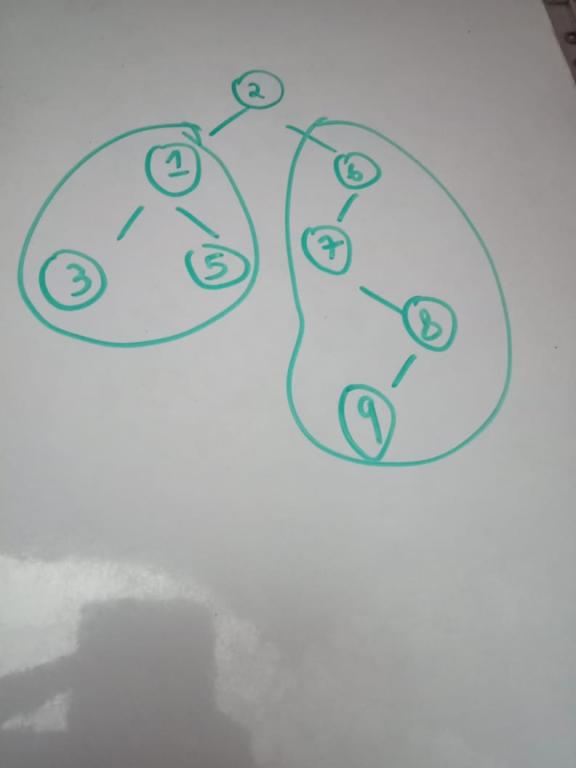
Now what all will change if we root the vertex 1 instead of 2 ?
Let's see
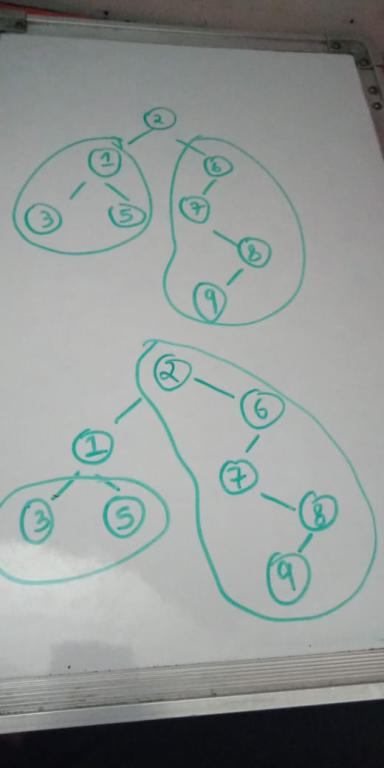
Firstly lets deal with the changes of vertex 2 . Its size changes and it's dp changes so dp[2] -= dp[1] (we remove the left subtree's contribution here) dp[2] -= sz[1] (remember that size also contributed in the inital answer so we need to remove it now) sz[2] -= sz[1] (remove the size finally , dont update this before updating dp[2] due to obv reasons)
Now we have successfully dealt with the changes in the vertex 2 so now we can get the answer with tree rooted at 1 by updating it's previous values as follows dp[1] += dp[2] dp[1] += sz[2] (Because now the size of 1 is no longer just 3 but 9 as its our new root so we update that too.)
This way we can check for each vertex the max points we can get and then finally choose maximum among all of them.
Hope it Helped.
If it did plz upvote :p






