What's a Voronoi Diagram?
Given a set $$$S$$$ of $$$n$$$ points in the 2D plane, the Voronoi diagram is a partition of the plane into regions. The region associated with a point $$$p\in S$$$ contains precisely the points $$$q$$$ such that $$$q$$$ is closer to $$$p$$$ than any other point in $$$S$$$. In other words, a point $$$q$$$ belongs to the region of its nearest neighbor.

The Voronoi diagram can be represented by the planar graph of boundaries between regions. A vertex in this graph is where three or more segments meet (or a point at infinity), and an edge is a segment connecting two of these vertices. The way the regions were defined, we see that a segment contains the points equidistant to two points in $$$S$$$, so it is part of their perpendicular bisector. Similarly, a Voronoi vertex is equidistant to three or more vertices in $$$S$$$, so it is their circumcenter. Recall that the circumcenter is the intersection of perpendicular bisectors.
What's a Delaunay Triangulation?
The Delaunay triangulation is the dual graph of the Voronoi diagram. That is, a Voronoi vertex is a Delaunay face and a Delaunay vertex is a Voronoi vertex. A Delaunay edge connects two points if and only if their corresponding Voronoi regions share a border.
In the following image, the set $$$S$$$ corresponds to the black points. The red vertices and edges are the Voronoi diagram. The black points and edges are the Delaunay triangulation.
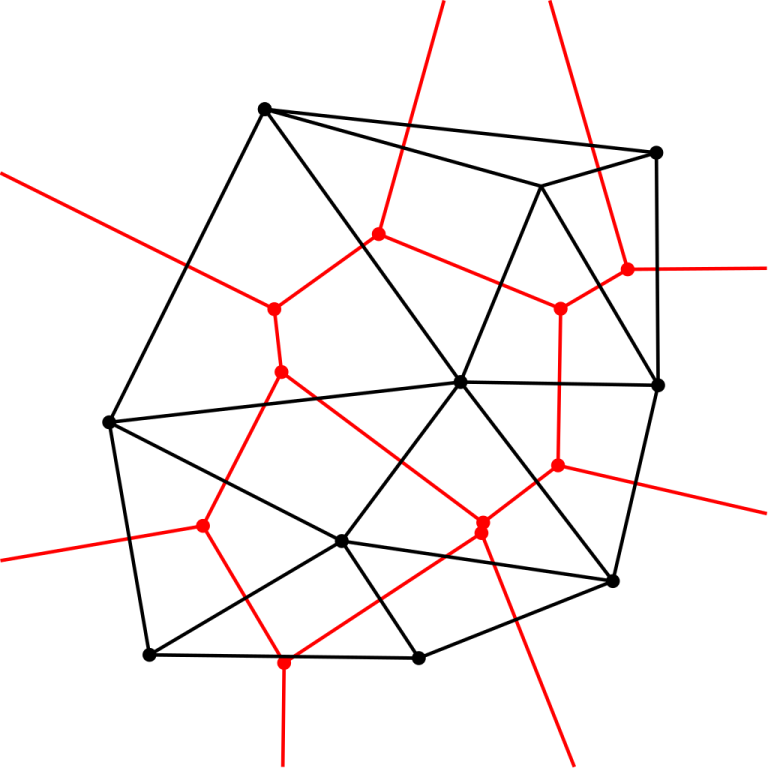
The Delaunay triangulation only involves edges between existing points, while the Voronoi diagram creates new vertices and needs a way to represent edges going infinitely in one direction. For this reason, it is often more convenient to compute the Delaunay triangulation and only convert to the Voronoi diagram if needed.
Why are these useful?
The definition of the Voronoi diagram immediately shows signs of applications. Given a set $$$S$$$ of $$$n$$$ points and $$$m$$$ query points $$$p_1,\ldots, p_m$$$, we can answer for each query point, its nearest neighbor in $$$S$$$. This can be done in $$$O((n + q)\log(n+q))$$$ offline by sweeping the Voronoi diagram and query points. Or it can be done online with persistent data structures.
Other than this, the Delaunay triangulation has many amazing properties of its own that can make it extremely useful for solving problems.
- For each Delaunay triangle, its circumcircle does not strictly contain any points in $$$S$$$. (In fact, you can also consider this the defining property of Delaunay triangulation)
- The number of Delaunay edges is at most $$$3n-6$$$, so there is hope for an efficient construction.
- Each point $$$p\in S$$$ is adjacent to its nearest neighbor with a Delaunay edge.
- The Delaunay triangulation maximizes the minimum angle in the triangles among all possible triangulations.
- The Euclidean minimum spanning tree is a subset of Delaunay edges.
Degenerate Cases
Because this is geometry, there are some degenerate cases I have hidden from you up to this point. The first case is when all the points in $$$S$$$ are contained in a line. In this case, the Voronoi diagram has all edges connecting two points at infinity, and the Voronoi diagram is disconnected (in all other cases it's connected). Also in this case, the dual graph is no longer a triangulation. We may still decide to represent it by the path of edges connecting the points.
Another nasty case is cocircular points. Here, there are Voronoi vertices where more than three segments intersect. In this case, the dual graph has a face with more than three sides. However, we want it to be a triangulation, so we can also say that any triangulation of such faces is valid, and we will allow non-unique Delaunay triangulations.
Algorithms
Many algorithms exist to compute the Delaunay triangulation and/or Voronoi diagram of a set of points. Each have their advantages and disadvantages.
Flip Algorithms
In this approach, you start with an arbitrary triangulation of the points. Then you repeatedly fix adjacent triangle pairs until the triangulation has the Delaunay property. The main advantage of this method is its simplicity: an arbitrary triangulation can be constructed with an incremental convex hull algorithm, and the disadvantage is that it could require $$$\Omega(n^2)$$$ flips in the worst case.
Incremental Algorithms
In this approach, you always maintain the Delaunay triangulation of a subset of the points and insert the points one at a time. When a point is inserted, you should delete all triangles whose circumcircle contains the newly added point. After deleting this connected set of triangles, you should repair the face it exposes. For each edge in this exposed face, you should add a triangle with that edge and the new point. This gives the straightforward $$$O(n^2)$$$ Bowyer-Watson algorithm.
If we insert the points in a random order, we can significantly reduce the number of triangle insertions and deletions. But to get expected $$$O(n\log n)$$$ runtime, we would need to avoid processing all the unaffected triangles. And this makes the implementation far more challenging. We need to maintain a search structure of the triangles in order to locate which one contains the new point.
The advantage of this method is that it achieves expected $$$O(n\log n)$$$ runtime with only integer computations, and the construction is online. The disadvantage is that it has a bad constant, isn't deterministic, and the triangle search structure can make for a tricky implementation.
Divide and Conquer
The divide and conquer algorithm first sorts the points by $$$x$$$-coordinate. Then it splits the points into two sets, recursively computes their Delaunay triangulations, and merges them together. As long as you can perform the merge in $$$O(n)$$$ time, the overall algorithm is $$$O(n\log n)$$$. When merging the triangulations, it is actually quite hard to keep track of the important adjacency information. The most popular strategy is perhaps the Quad-Edge data structure.
The advantage is that this gives a deterministic $$$O(n\log n)$$$ algorithm with only integer computations. The disadvantage is the complexity of the quad-edge data structure and the costly memory usage that comes with it.
3D Convex Hull Reduction
An interesting fact is that the problem of Delaunay triangulation can be reduced to 3D convex hull. If for each point $$$(x,y)$$$ we also give it the $$$z$$$-coordinate $$$x^2+y^2$$$ and compute the 3D convex hull, then the downward-facing convex hull faces correspond exactly to the Delaunay triangles. The advantage is that if you happen to have a good 3D convex hull implementation, you get Delaunay triangulation for free. The disadvantages are that $$$O(n\log n)$$$ 3D convex hull is a whole beast of its own, and the large $$$z$$$-coordinates will exacerbate precision and overflow errors in the 3D convex hull implementation. The main strategies for 3D convex hull are incremental and divide-and-conquer algorithms, which are only more complicated than their counterparts in the special case of Delaunay triangulation.
My previous blog on 3D convex hull gave an $$$O(n\log n)$$$ randomized incremental implementation, but it turns out to have quite a bad constant for practical use.






