I hope you enjoyed this round! All three problems are relatively old, initially being prepared by me between 2020 and early 2021.
103503A — Make Sum Great Again
Author: Gheal
It is always optimal to add the smallest integer which is not already in the array.
The number of operations will never exceed $$$\sqrt{2 \cdot s}.$$$
Based on the first hint, the final array will be equal to $$${v_1,v_1,\ldots, v_n} \cup [1,x]$$$, for some $$$x$$$.
Hint 4: How can we find the value of $$$x$$$ faster than $$$O(\sqrt{s})$$$?
Lemma: The number of operations will never exceed $$$\sqrt{2 \cdot s}$$$.
Since we need to maximize the final length of the array, it is always optimal to add the smallest integer which is not already present in $$$a$$$.
The naive implementation of this idea has a runtime complexity of $$$O(n \cdot \sqrt s)$$$, although this can be easily optimized to $$$O((n+ \sqrt s)log(n))$$$, if binary search is used to check whether the new elements are already present in $$$a$$$.
The optimal solution has a runtime complexity of $$$O(N log S)$$$. Based on hints $$$3$$$ and $$$4$$$, we can find the value of $$$x$$$ with binary search. For some $$$x$$$, the sum of the elements in $$$a$$$ will be equal to $$$sum(x)=\frac{x\cdot(x+1)}{2}+\sum_1 v_i$$$, where $$$\sum_1 v_i$$$ is the sum of the elements greater than $$$x$$$.
Since the sum of elements $$$sum(x)$$$ is a monotonous function, we can use binary search on the interval $$$[1,\sqrt{2 \cdot s}]$$$ to find the exact value of $$$x$$$.
Final time complexity: $$$O(N log S)$$$
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll NMAX=2e5+5;
ll v[NMAX];
int main()
{
ios_base::sync_with_stdio(false); cin.tie(0);
ll n,s;
cin>>n>>s;
for(ll i=0;i<n;i++)
cin>>v[i];
ll l=0,r=2e9,ans=0;
while(l<=r){
ll m=(l+r)/2;
ll sum=m*(m+1)/2;
for(ll i=0;i<n;i++)
if(v[i]>m)
sum+=v[i];
if(sum>=s)
ans=m,r=m-1;
else
l=m+1;
}
ll len=ans;
for(ll i=0;i<n;i++)
len+=(v[i]>ans);
cout<<len;
return 0;
}
103503B — Binary Search Search
Author: Gheal
The numbers are printed in ``layers''.
Try to represent the layers as a binary tree.
To better understand the solution, let's consider $$$n=12$$$. The final array is the BFS traversal starting from the root of the following binary tree:
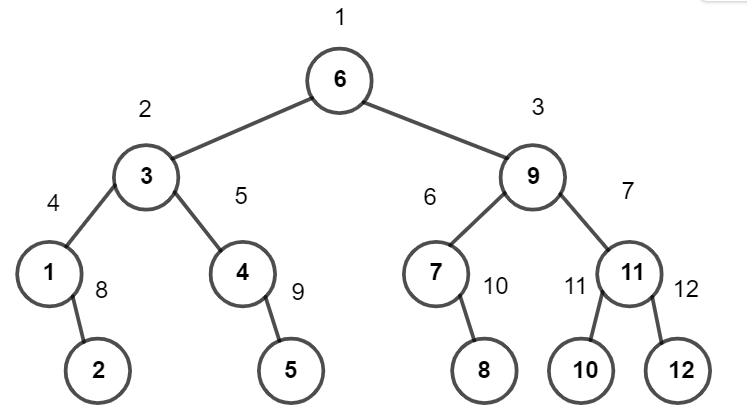
This binary tree was generated by starting with the root $$$m=\lfloor \frac{n+1}{2} \rfloor=6$$$. Each node $$$m=\lfloor \frac{l+r}{2}\rfloor$$$ has up to two children: $$$m_1=\lfloor \frac{l+(m-1)}{2} \rfloor$$$ and $$$m_2=\lfloor \frac{r+(m+1)}{2} \rfloor$$$.
If our given integer $$$k$$$ is in a complete layer, then we can employ a binary search-type algorithm to find the position of $$$k$$$:
l = 1, r = n, position = 1, visited_nodes = 1
while(visited_nodes<=n){
m = (l + r) / 2
if(k==m){
print position
return
}
if(k<m) position = position * 2
else position = position * 2 + 1
visited_nodes = visited_nodes * 2 + 1
}
This algorithm has the added benefit of not printing anything if $$$k$$$ is not in a complete layer. In this case, the position of $$$k$$$ in the last layer can be determined from $$$position$$$, although this isn't very straightforward. If the binary tree were complete, then the position of $$$k$$$ in the last layer would be $$$position-\frac{\text{visited_nodes}-1}{2}$$$, since there are $$$\frac{\text{visited_nodes}-1}{2}$$$ nodes on the other layers, all of which will be printed before $$$k$$$.
By looking at the missing nodes from the binary tree for $$$n=12$$$, one may make the crucial observation that the general case position for $$$k$$$ in the last layer is equal to $$$k-(position-\frac{\text{visited_nodes}-1}{2})$$$.
In conclusion, the final position for $$$k$$$ will be $$$k-(position-\frac{\text{visited_nodes}-1}{2})+\frac{\text{visited_nodes}-1}{2}=k+\text{visited_nodes}-position-1$$$.
Time complexity per testcase: $$$O(log n)$$$
#include<bits/stdc++.h>
#define NMAX 1000005
using namespace std;
typedef long long ll;
void tc(){
ll n,p;
cin>>n>>p;
ll cntLess=0,cnt=1,currentId=1;
ll l=1,r=n;
while(cnt<=n){
ll m=(l+r)/2;
cntLess=cntLess*2+(p>=m);
if(m==p){
cout<<currentId<<' ';
return;
}
else if(p<m) r=m-1,currentId*=2;
else l=m+1,currentId=currentId*2+1;
cnt=cnt*2+1;
}
cout<<p+cnt/2-cntLess<<' ';
}
int main()
{
ios_base::sync_with_stdio(false); cin.tie(0);
int t;
cin>>t;
while(t--)
tc();
return 0;
}
#include <bits/stdc++.h>
using namespace std;
long long dfs(pair<long long, long long> interv, long long k) {
long long mid = (interv.first + interv.second) / 2;
if (k == mid) {
return 1ll;
}
if (k < mid) {
return 1ll + dfs({ interv.first,mid - 1 }, k);
}
else {
return 1ll + dfs({ mid + 1,interv.second }, k);
}
}
long long count(pair<long long, long long> interv, long long lvl) {
long long lg = interv.second - interv.first + 1;
return min((1ll << (lvl - 1)), lg - ((1ll << (lvl - 1)) - 1));
}
long long solve(pair<long long, long long> interv, long long k, long long lvl) {
long long mid = (interv.first + interv.second) / 2;
if (mid == k) {
return 1;
}
if (mid < k) {
return count({ interv.first,mid - 1 }, lvl - 1) + solve({ mid + 1,interv.second }, k, lvl - 1);
}
else {
return solve({ interv.first,mid - 1 }, k, lvl - 1);
}
}
long long solve_brute(long long n, long long k) {
vector<long long> a(n + 1);
long long p = 0;
queue<pair<long long, long long>> q;
q.push({ 1,n });
while (!q.empty()) {
pair<long long, long long> current = q.front();
long long mid = (current.first + current.second) / 2;
a[++p] = mid;
if (mid > current.first) {
q.push({ current.first , mid - 1 });
}
if (mid < current.second) {
q.push({ mid + 1,current.second });
}
q.pop();
}
for (long long i = 1; i <= n; ++i) {
if (a[i] == k) {
return i;
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
long long q;
cin >> q;
while (q--) {
long long n, k;
cin >> n >> k;
long long lvl = dfs({ 1,n }, k);
cout << ((1ll << (lvl - 1)) - 1) + solve({ 1,n }, k, lvl) << ' ';
}
}
103503C — Plates
Author: Gheal
Any final configuration can be uniquely determined by a permutation of $$${1,2,3,\ldots, k}$$$
$$$k \le 20$$$
Let dp[mask] be the minimum number of moves required to cover the first $$$\Sigma_{i=1}^k getBit(mask,i)*p_i$$$ slots with all plates of colours $$$c_1,c_2,\ldots$$$ where $$$getBit(mask,c_i)=1, \forall i$$$. Naturally, $$$dp[0]=0$$$.
Transitioning from $$$dp[mask]$$$ to $$$dp[mask+2^k]$$$, where $$$getBit(mask,k)=0$$$ can be done fairly easily. Let $$$pos=\Sigma_{i=1}^k getBit(mask,i)*p_i$$$ and $$$cntdiff(l,r,k)$$$ be the number of plates in the initial configuration $$$a_i$$$ which satisfy the following requirements:
- $$$l \le i \le r$$$;
- $$$a_i \neq 0$$$;
- $$$a_i \neq k$$$.
From these definitions, the value of $$$dp[mask+2^k]$$$ can be computed using the following formula:
$$$cntdiff(l,r,k)$$$ can be calculated in $$$O(1)$$$ per query using prefix sums. Calculating the prefix sums has a time complexity of $$$O(n \cdot k)$$$.
Intended time complexity: $$$O(n\cdot k + 2^k \cdot k)$$$
Reconstructing the final configuration will also require an auxiliary array $$$prev[mask]$$$ — the last colour added to $$$mask$$$.
#include<bits/stdc++.h>
using namespace std;
const int NMAX=1e5+1,KMAX=21;
int dp[1<<KMAX],lastAdded[1<<KMAX],cnt[KMAX],n,k;
bool visited[1<<KMAX];
int freq[NMAX][KMAX];
int cnteq(int l, int r, int num){
if(r<l)
return 0;
return freq[r][num]-(l?freq[l-1][num]:0);
}
int cntdiff(int l, int r, int num){
if(r<l)
return 0;
return r-l+1-cnteq(l,r,num)-cnteq(l,r,0);
}
void iterativeBt(){
queue<pair<int,int>> q; /// (bitmask, pos)
q.push({0,0});
visited[0]=1;
while(!q.empty()){
int bm=q.front().first,pos=q.front().second;
for(int i=0;i<k;i++){
if(!(bm>>i&1)){
if(dp[bm]+cntdiff(pos,pos+cnt[i]-1,i+1)<dp[bm|(1<<i)]){
lastAdded[bm|(1<<i)]=i;
dp[bm|(1<<i)]=dp[bm]+cntdiff(pos,pos+cnt[i]-1,i+1);
}
if(!visited[bm|(1<<i)]){
q.push({bm|(1<<i),pos+cnt[i]});
}
visited[bm|(1<<i)]=1;
}
}
q.pop();
}
}
int main()
{
for(int i=1;i<(1<<KMAX);i++) dp[i]=INT_MAX; /// dp[0]=0
scanf("%d%d",&n,&k);
for(int i=0;i<n;i++){
int x;
scanf("%d",&x);
if(i) for(int j=0;j<=k;j++)
freq[i][j]=freq[i-1][j];
freq[i][x]++;
}
for(int i=0;i<k;i++){
scanf("%d",&cnt[i]);
}
iterativeBt();
stack<int> ans; int pos=(1<<k)-1;
printf("%d\n",dp[pos]);
while(pos){
ans.push(lastAdded[pos]);
pos^=(1<<lastAdded[pos]);
}
while(!ans.empty()){
for(int i=0;i<cnt[ans.top()];i++)
printf("%d ",ans.top()+1);
ans.pop();
}
return 0;
}





