Третий отборочный раунд и его разбор были подготовлены Chmel_Tolstiy, aropan, Romka, SobolS, Ra16bit, snarknews и Gassa.
В третьем раунде турнира «Яндекс.Алгоритм» хотя бы одну попытку сделало 265 участников, хотя бы одну задачу из них решило 177. По задаче A было сделано 559 попыток, из них 137 успешных, по задаче B — 127 попыток (47 успешных), по задаче C — 111 попыток (64 успешных), по задаче D — 64 попытки (15 успешных), по задаче E — 45 попыток (20 успешных) и по задаче F — 606 попыток (129 успешных).
Задачи третьего раунда в среднем оказались проще, чем задачи первых двух раундов, и по ходу тура стало понятно, что победитель, по всей видимости, решит все задачи. Действительно, на 72-й минуте шесть задач сдал Petr, правда, все задачи были сданы «в открытую». За пять минут до конца турнира на второе место с шестью задачами выходит KADR, у которого также все задачи сданы «в открытую». Но практически сразу шестую задачу сдаёт nkurtov (Николай Куртов, Швейцария) и выходит на первое место, так как у него сданы «втёмную» три задачи. За две минуты до конца турнира на второе место выходит winger, у которого две задачи в начале турнира были сданы «втёмную», а остальные — «в открытую». И наконец на последней минуте задачу Е «втёмную» сдаёт s.quark (s-quark) из Китая и выходит на первое место: из шести решённых задач у него «в открытую» сдана только B. Итого до системных тестов все задачи решили пятеро участников. Лидирует s.quark, за ним — nkurtov, за ним — winger, Petr — на четвёртом месте, KADR — на пятом.
После системных тестов выясняется, что у s.quark не прошла задача F, которую он сдавал «втёмную» на 25-й минуте, у nkurtov не прошли сразу две задачи — С и D. У winger прошли обе сданные «втёмную» задачи, таким образом, он занял первое место в третьем раунде. Второе место занял Petr, который уже обеспечил себе выход в финал по итогам первого раунда. KADR остался на третьем месте, ainu77 (ainu7) из Южной Кореи переместился на четвёртое, а s.quark даже после того, как у него не прошла задача, оказался на пятом месте и попал в число четырёх финалистов по итогам раунда.
Задача A (Конфетное настроение)
Подсчитаем количество невкусных конфет. Пусть их будет M. Тогда если M = 0, то ответ равен  . Иначе рассмотрим, какой ожидаемый вклад в изменение настроения даст i-я конфета, если она вкусная. Она может находиться равновероятно в M + 1 позиции относительно невкусных конфет, и только в одной из них вкусная конфета будет съедена. Значит, ожидаемый вклад в изменение настроения от одной вкусной конфеты Ai равен
. Иначе рассмотрим, какой ожидаемый вклад в изменение настроения даст i-я конфета, если она вкусная. Она может находиться равновероятно в M + 1 позиции относительно невкусных конфет, и только в одной из них вкусная конфета будет съедена. Значит, ожидаемый вклад в изменение настроения от одной вкусной конфеты Ai равен 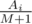 . Для невкусных конфет ожидаемый вклад в изменение настроения равен
. Для невкусных конфет ожидаемый вклад в изменение настроения равен 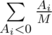 , так как первой невкусной конфетой может оказаться равновероятно любая из невкусных. В итоге математическое ожидание изменения настроения равно
, так как первой невкусной конфетой может оказаться равновероятно любая из невкусных. В итоге математическое ожидание изменения настроения равно 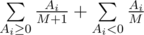 .
.
Задача B (Шарики)
Для определенности будем считать, что N ≤ M.
Рассмотрим случай, когда N = 1. Пусть на фото находится k шариков. Заметим, что можно оставить любые k шариков. Однако не любое их относительное расположение может быть получено, потому как невозможно поменять их относительный порядок. Но при этом на любых k позициях можно разместить оставшиеся шарики. Следовательно, всего различных фото можно получить 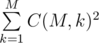 .
.
Пусть N ≥ 2. Тогда если на фото k = N·M шариков, то такое фото можно получить только одно, так как мы не делали ни одного хода (первый ход обязательно убирает один шарик с поля). Если k = N·M - 1, то после первого хода можно ходить только в свободную клетку на поле — это эквивалентно известной головоломке «Пятнашки»; в этом случае ровно половина перестановок будет достижима (см. ссылку выше). Если k < N·M - 1, то рассмотрим две любые пустые клетки, первым делом получим конфигурацию, в которой пустые клетки стоят рядом. Тогда относительно одной из них головоломка «Пятнашки» разрешима (требуется четность суммы количества инверсий в перестановке с номером строки и столбца, а у выбранных пустых клеток сумма номеров строки и столбца отличается на 1). Далее, выбрав в качестве пустой клетки подходящую, остается только собрать головоломку.
Таким образом, общее количество фотографий 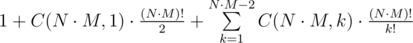 .
.
Задача C (Размещение болельщиков)
Наиболее простой способ решения этой задачи заключался в генерации всех возможных относительных перестановок болельщиков. Зафиксируем некоторый порядок болельщиков, к примеру, снизу вверх, и пусть i-й по счёту болельщик имеет исходный номер pi. Понятно, что если каждому болельщику не мешает тот, кто сидит непосредственно перед ним, то все болельщики видят поле. Рассмотрим все пары подряд идущих болельщиков. Если hpi ≤ hpi + 1, то никаких ограничений на рассадку эта пара болельщиков не накладывает: где бы ни сидел болельщик с номером pi + 1, ему никогда не будет мешать сидящий перед ним болельщик номер pi, поскольку он меньше ростом. Если же hpi > hpi + 1, то появляется следующее ограничение: болельщик с номером pi + 1 не может занимать следующие hpi - hpi + 1 мест после болельщика с номером pi, иначе ему не будет видно поля. Соответственно, эти hpi - hpi + 1 рядов нужно убрать из рассмотрения для данного зафиксированного порядка болельщиков. Проделав эту операцию для всех пар болельщиков, сидящих друг за другом, нужно прибавить к ответу количество сочетаний из оставшегося количества мест по K, где K — это общее количество болельщиков. Для того чтобы быстро выполнять эту операцию, нужно заранее рассчитать таблицу значений Cnk для n и k, не превосходящих 1000.
Сложность решения: O(n2 + k!·k).
Также при желании задачу можно было решать и более сложным способом, а именно методом динамического программирования, где состоянием являлась тройка «сколько рядов рассмотрели, маска уже посаженных болельщиков, номер последнего болельщика». Переход в данном случае заключался в переборе «предпоследнего посаженного болельщика». Для быстрой работы этого решения параллельно с подсчётом таблицы ДП нужно было сохранять таблицу кумулятивным сумм, чтобы избавиться от вложенного цикла по рядам.
Задача D (Интересный язык)
Сначала опишем переборное решение. Найдём все пары слов, для которых одно слово является началом другого. Удалим меньшее слово из большего, оставив только суффикс. Если для каждого суффикса посчитать, сколько раз его можно получить такой операцией, и обозначить это число через cntsuff, то отсюда получаем ответ на задачу: это 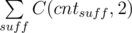 , где суммирование ведётся по всем суффиксам.
, где суммирование ведётся по всем суффиксам.
Для того чтобы посчитать для каждого суффикса такое количество пар, воспользуемся бором (для справки см. алгоритм Ахо-Корасик на сайте e-maxx, раздел «Бор. Построение бора»). Построим по входному набору слов два бора: один будет содержать все слова, как они заданы во входных данных, а другой будет содержать перевёрнутые слова. Обойдём бор, содержащий перевёрнутые слова. Каждый раз, когда мы будем заходить в терминальную вершину, поднимемся из этой вершины вверх до корня, параллельно спускаясь по таким же символам в боре, содержащем исходные слова. Если в процессе этого подъёма/спуска мы попадаем в терминальную вершину в боре с исходными словами, то мы должны увеличить на один счётчик для суффикса, в котором сейчас находимся в боре с перевёрнутыми словами. Если в процессе подъёма мы вышли из бора с исходными словами, подъём можно прекратить.
После такого обхода бора для каждого суффикса в соответствующей вершине бора будет записано корректное значение величины cntsuff, и останется только посчитать ответ по формуле, описанной выше.
Сложность решения: O(sumL), где sumL — суммарная длина всех слов.
Задача E (Дорожный вопрос)
Давайте посмотрим, что нам даёт уплата налога в некотором городе. После того как мы заплатили налог в городе A, некоторые города мы теперь можем посетить бесплатно. В число этих городов входят те, которые, во-первых, достижимы из города A, во-вторых, из которых достижим город A. Если перейти от городов к теории графов, то можно сказать, что мы теперь можем бесплатно посещать все вершины, которые входят в ту же сильно связную компоненту, что и город A. Таким образом, если разбить исходный граф на сильно связные компоненты, то налог можно платить только на въезде в каждую компоненту. Поскольку въезд в компоненту сильной связности «открывает» для бесплатного путешествия всю эту компоненту, а все налоги неотрицательные, то никогда не будет выгодно добровольно платить налог в каком-то другом городе этой же сильно связной компоненты.
Построим новый граф на основании исходного. Его вершины будут соответствовать сильно связным компонентам исходного графа. Веса рёбер нужно расставить следующим образом: для каждой пары сильно связных компонент, между вершинами которых есть ребро в исходном графе, нужно создать ребро в новом графе с весом, равным минимуму из величин налогов в городах, в которые входят ребра, связывающие эти две сильно связные компоненты. При этом, естественно, нужно учитывать ориентацию исходных рёбер.
После того как новый граф построен, нужно найти в нём кратчайший путь между теми вершинами, которые соответствуют сильно связным компонентам, содержащим вершины 1 и n исходного графа. Это можно сделать либо алгоритмом Дейкстры, либо методом динамического программирования, учитывая то, что полученный в результате сжатия сильно связных компонент граф не имет циклов. Также отдельно нужно рассмотреть начало путешествия, поскольку налог можно по условию задачи платить только в момент въезда в какой-то город.
Задача F (Место под столицу)
Если угол между радиусами больше двух радиан, то минимальное расстояние — сумма радиусов. Иначе, разность радиусов плюс длина дуги окружности, проходящей через точку с меньшим радиусом. Это следует из того факта, что в «криволинейной трапеции», составленной из двух радиальных рёбер и двух дуг, кратчайшим расстоянием между противоположными вершинами является путь по радиальному ребру и дуге меньшего радиуса.
Остаётся просто аккуратно провести все вычисления; использование функции atan2() позволяет обойти большинство «подводных камней». Без использования atan2() проблемы с точностью возникают в случае двух близких точек с большими радиусами; в этом случае помогает вместо арккосинуса во избежание потерь точности использовать арксинус.











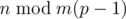 — хорошее. Рассчитаем и запомним в таблице для каждого
— хорошее. Рассчитаем и запомним в таблице для каждого 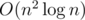 .
.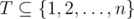 ассистентом и выполняет остальные задачи сам (но необязательно в последовательные дни), то существует оптимальное расписание, в котором профессор передает задачи из подмножества
ассистентом и выполняет остальные задачи сам (но необязательно в последовательные дни), то существует оптимальное расписание, в котором профессор передает задачи из подмножества 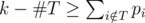 .
.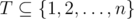 за дни после
за дни после 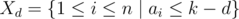 — множество задач, которые могут быть переданы в день
— множество задач, которые могут быть переданы в день 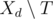 непусто, то мы можем в день
непусто, то мы можем в день 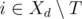 , которая максимизирует значение
, которая максимизирует значение 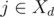 (так как ассистент выполнит задачу в срок) и
(так как ассистент выполнит задачу в срок) и 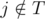 (мы предполагаем, что расписание
(мы предполагаем, что расписание 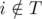 и
и 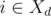 ). Иначе, если
). Иначе, если 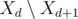 в кучу (то есть задачи с
в кучу (то есть задачи с  .
.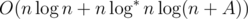 .
. для обозначения получающихся частей. Решение этой задачи получается в три шага.
для обозначения получающихся частей. Решение этой задачи получается в три шага.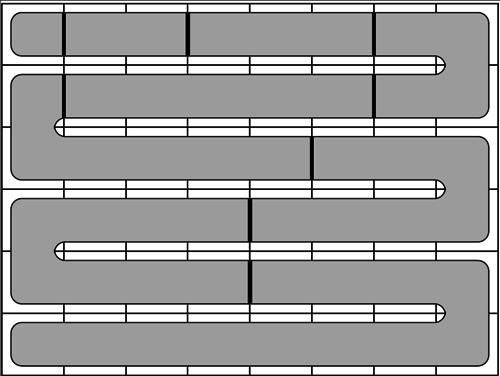

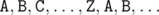 в том порядке, в котором части появляются на змейке. Однако в некоторых случаях такой способ не работает.
в том порядке, в котором части появляются на змейке. Однако в некоторых случаях такой способ не работает. . Пусть
. Пусть 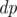 , где
, где 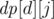 — истина если и только если делитель
— истина если и только если делитель 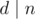 :
: 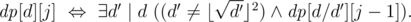
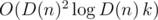 (логарифм появляется из-за использования структуры map или аналогичной для хранения делителей
(логарифм появляется из-за использования структуры map или аналогичной для хранения делителей 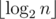 , что в нашем случае не более 29. Действительно, для
, что в нашем случае не более 29. Действительно, для 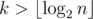 ответ всегда «NO» (доказательство следует из следующего решения).
ответ всегда «NO» (доказательство следует из следующего решения).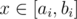 тогда и только тогда, когда возможно добиться того, чтобы на
тогда и только тогда, когда возможно добиться того, чтобы на 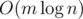 .
.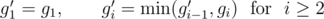
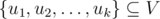 представлять собой одну или более связных компонент графа в данный момент времени.
представлять собой одну или более связных компонент графа в данный момент времени.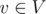 мы храним в ячейке массива
мы храним в ячейке массива 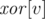 результат операции
результат операции 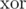 , примененной к весам всех ребер, инцидентных этой вершине. Заметим, что такие значения можно обновлять за время
, примененной к весам всех ребер, инцидентных этой вершине. Заметим, что такие значения можно обновлять за время 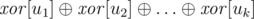
 обозначает операцию
обозначает операцию 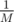 , где
, где  такое же число, но при этом разрешим стикерам выходить за границу и накрывать позиции из
такое же число, но при этом разрешим стикерам выходить за границу и накрывать позиции из  стикеров.
стикеров.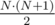 .
. . Существует быстрый способ посчитать
. Существует быстрый способ посчитать 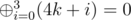 . Значит,
. Значит, 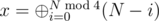 .
. . Значит, чтобы из кучки
. Значит, чтобы из кучки 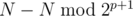 , их ровно половина. Если в
, их ровно половина. Если в 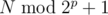 .
.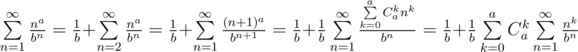
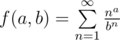 , имеем
, имеем 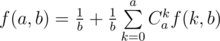
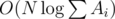 . Также следует учесть, что нужно предварительно отсортировать темы по значению
. Также следует учесть, что нужно предварительно отсортировать темы по значению 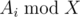 для поиска тем с максимальным количеством задач, когда у Гены уже нет возможности решать по
для поиска тем с максимальным количеством задач, когда у Гены уже нет возможности решать по 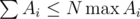 , и свойств логарифма, получается
, и свойств логарифма, получается 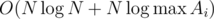 .
.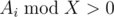 .
.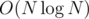 .
.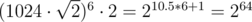 , и вычисления можно производить в беззнаковых 64-битных целых. При этом при сравнении дробей потребуется или использовать встроенные типы для работы с длинными числами (в тех языках, в которых они есть), либо использовать модулярную арифметику, либо вычислять НОД, либо хранить старшую часть числа отдельно...
, и вычисления можно производить в беззнаковых 64-битных целых. При этом при сравнении дробей потребуется или использовать встроенные типы для работы с длинными числами (в тех языках, в которых они есть), либо использовать модулярную арифметику, либо вычислять НОД, либо хранить старшую часть числа отдельно...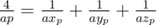 . Таким образом, достаточно сначала предпросчётом построить таблицу для всех простых чисел и для
. Таким образом, достаточно сначала предпросчётом построить таблицу для всех простых чисел и для 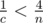 , то
, то 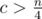 . Так как
. Так как 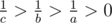 , а значит
, а значит 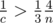 , тем самым
, тем самым 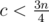 ; из аналогичных соображений
; из аналогичных соображений 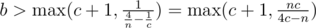 и
и 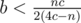 . Соответственно, перебираем для всех простых
. Соответственно, перебираем для всех простых 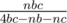 . При этом размер кода не будет превосходить 50k, что меньше, чем source limit.
. При этом размер кода не будет превосходить 50k, что меньше, чем source limit. в сумму двух «египетских» дробей, использовав алгоритм Фибоначчи; в этом случае решение укладывается в Time Limit без предрасчёта (именно такие решения и сдали оба участника, решивших задачу).
в сумму двух «египетских» дробей, использовав алгоритм Фибоначчи; в этом случае решение укладывается в Time Limit без предрасчёта (именно такие решения и сдали оба участника, решивших задачу).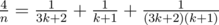 ,
,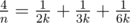 ,
,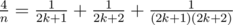 ,
,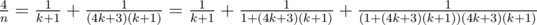 ,
,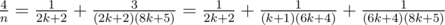 .
.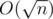 . Можно также изначально разложить число
. Можно также изначально разложить число 


