Catalan Numbers is a well known sequence of integers that appear in combinatorics, there is a chance that you might have run into such counting problems and you might have even solved them with DP without realizing that they are a known sequence. Here is a problem to get us started.

Binary Trees Count

Find the count of different binary trees with $$$n$$$ nodes, we'll denote to that by $$$C_n$$$. This can be solved by observing the substructure of the problem:

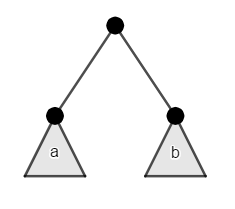
From the root, the left subtree $$$a$$$ can be any binary tree of size $$$x$$$, the right subtree $$$b$$$ can be any binary tree of size $$$y$$$, such that $$$x+y=n-1$$$ (as we took one node as the root). With the base case at $$$C_0=1$$$ as the empty tree is a valid tree of size $$$0$$$. This directly gives us the answer by the following recurrence relation: (Segner's recurrence relation)

The sequence of numbers $$$C_0, C_1, C_2, ...$$$ is called Catalan Numbers, and for reference they are: $$$1, 1, 2, 5, 14, 42, ...$$$.

This gives us a simple $$$O(n^2)$$$ implementation with DP, however can we do better? In fact we can, this simple recurrence formula gives out the same values:

According to: https://codeforces.net/blog/entry/68204

MikeMirzayanov announced a way to uphack recent problems for Div.1 participants. I'm curious to listen to the details on why this is limited only to last week problems. He clarified why it was limited to Div.1 participants but not why only recent problems.

I mean, for instance I believe that Educational Round 3B is hackable with this test case (as many participants don't use long long for the length of the frog's tongue):

1 200000
1 0
1 1000000000
1 1000000000
1 1000000000
...

So what is the harm in enabling uphacking for old problems as well?

Hello :D

I'm trying to write a statement for a problem using Polygon, but there are so many things that should be easy in LaTex but yet are "unsupported" in polygon. Is there any documentation for what subset of LaTeX is available in Polygon for HTML statements?

Here is some of what I frequently need but polygon rejects, if you can help with the 'Polygonic' way to perform this, it would be awesome :D

• Insert a newline or a linebreak: tried both '\\' and '\newline'.
• A horizontal line: tried '\hbreak'
• A table: tried both '\begin{tablular}' and '\begin{table}'

• A matrix: tried '\begin{matrix}' and '\begin{array}':

So yeah, without a documentation on supported LaTeX commands, I get stuck way too often trying to find alternative solutions. Is there any help?

Also, is there a way to check the LaTeX code behind already existing problems? It would be much much easier to just find what I want and copy the format.

Me and MrOkasha found an odd quirk with the GNU G++ compiler, (we tested with G++11, G++14, and G++17, all having the same bug).

This code here:

#include <bits/stdc++.h>
using namespace std;

set<double> st;

int main() {

    double x, y;
    for(int i = 0; i < 3; ++i){
        cin >> x >> y;
        st.insert(y/x);
    }
    cout << st.size() << endl;
}
// input:    5 -2 5 -2 5 -2

should output without any doubt '1', as the set should remove duplicate numbers. The output is 3 for some reason on the GNU compilers. It should be noted that the output is indeed 1 on Clang++17 compiler, Visual C++, and other available versions of GNU G++ compilers found online, for us, it seems the bug only occurs here on codeforces, verified by the Custom Invocation feature.

The weirdest thing about this bug is that, for some bizarre reason, if the declaration of the set set<double> is moved to inside the main function, the code works as intended.

Any thoughts on this weird issue?