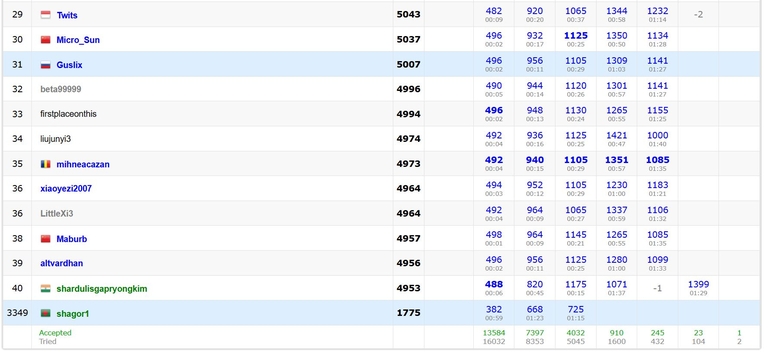
Results of some participants of Bangladesh highlighted as my own results, when I in page with results of my true account.
Do I have a split personality or it's a feature of Codeforces what I haven't been known?
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3845 |
| 2 | tourist | 3798 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3589 |
| 6 | Ormlis | 3532 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 10 | Um_nik | 3450 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 165 |
| 2 | Qingyu | 160 |
| 3 | -is-this-fft- | 159 |
| 4 | atcoder_official | 157 |
| 5 | Dominater069 | 156 |
| 6 | adamant | 154 |
| 7 | djm03178 | 151 |
| 8 | luogu_official | 149 |
| 9 | awoo | 147 |
| 10 | TheScrasse | 145 |

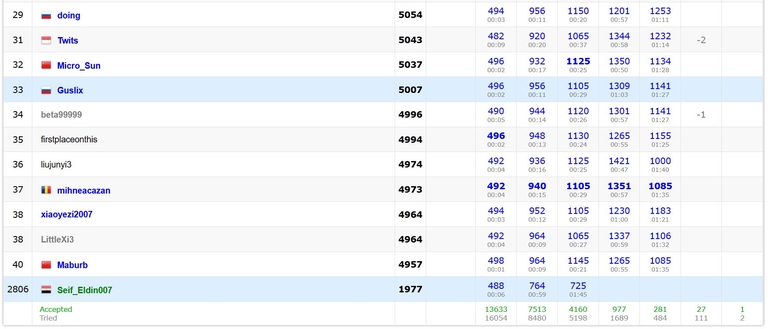
Results of some participants of Bangladesh highlighted as my own results, when I in page with results of my true account.
Do I have a split personality or it's a feature of Codeforces what I haven't been known?

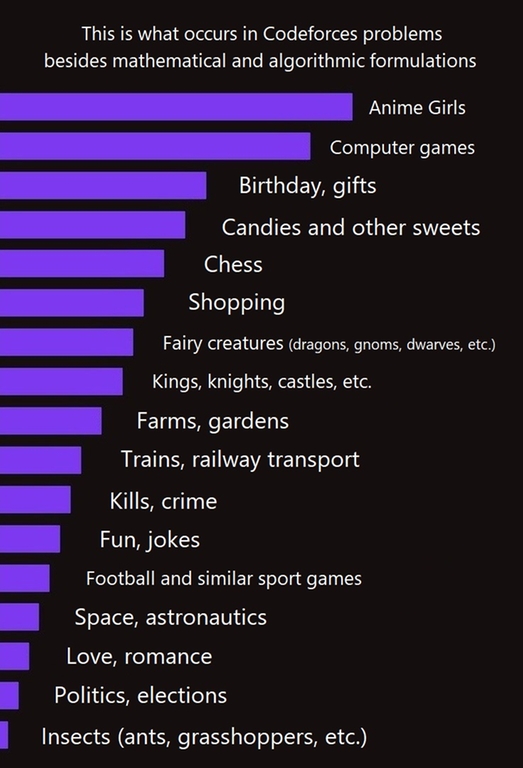
There are $$$O(\infty)$$$ different things that have mentioned in some problem statement on Codeforces and not only it. This is the top of the most interesting and common ones. Place distribution based on my observations
Thanks to creative problemsetters for so various and interesting world of competitive programming problems!
To get the next permutation of array of its subsegment there is a simple and very old Narayana's algorithm. This algorithm invented by Indian mathematician Pandit Narayana more than 600 years ago.
Given array $$$a$$$. How to go to its next permutation?
Find the longest non-increasing suffix of the array (LNIS). If whole array is non-increasing, permutations are exhausted.
Let LNIS be a suffix $$$k$$$, where $$$k$$$ is position where it begins. Swap previous element, $$$a_{k-1}$$$ and the next largest number (NLN) that exists in suffix $$$k$$$.
Reverse suffix $$$k$$$.
Time complexity: $$$O(n)$$$ in the worst case. But on average length LNIS is about 3 elements, so iteration over all permutations is doing for $$$O(n!)$$$, thus $$$O(1)$$$ for one permutation.
Although suddenly there is such a problem. Given an array of 100500 elements and 100500 queries to get next or previous permutation. If the array is sorted and first query is prev permutation on whole array, second query is next permutation on whole array, and further this loop is repeating; you must to walk over all array, answer each query for $$$O(n)$$$.
This algorithm can be implemented for $$$O(\log n)$$$ on a treap. Reversal is known, and swapping is just a combination of split and merge operations. Also we need to find LNIS and NLN. LNIS is sorted by definition, so we can apply binary search in order to find NLN of $$$a_{k-1}$$$.
Position $$$k$$$ of LNIS is found a recursive algorithm too. Let we in subtree $$$t$$$ now. First, find LNIS of right subtree of $$$t$$$. If the right subtree is not sorted in non-increasing order, we don't heed visit left subtree of $$$t$$$.
Else we should to compare value of root of $$$t$$$ with the first element of right subtree and the last element of left subtree. If still keeps a non-increasing order, continue the search in left subtree. To avoid additional costs, we need to maintain first and last elements and non-increasing order flag for each subtree and recalc it after each operation.
To get the previous permutation there's similar algorithm. Here is non-decreasing order instead of non-increasing one and next smallest element instead next largest one.
Time complexity: $$$O(\log n)$$$
struct node {
int val, heap_val, size; //size of this tree
node *l, *r; //left and right subtrees
bool reversed, non_incr, non_decr;
int first_elem, last_elem;
node(int Val=0) : val(Val), size(1), l(0), r(0), reversed(0) {
heap_val = rand() * (1<<15) + rand(); //now heap_val to 2^30
non_incr = non_decr = 1;
first_elem = last_elem = Val;
}
};
typedef node* treap;
treap root;
void lazy_pr(treap t){
if(!t || !t->reversed) return; //if the tree is nullptr or is already reversed even number of times
t->reversed=0;
swap(t->l, t->r), swap(t->non_incr, t->non_decr), swap(t->first_elem, t->last_elem);
if(t->l) t->l->reversed ^= 1; if(t->r) t->r->reversed ^= 1; //push to "children"
}
int get_size(treap t){
return t ? t->size : 0;
}
void recalc(treap t){
if(!get_size(t)) return;
t->size = get_size(t->l) + get_size(t->r)+1; //size
//first and last elements
lazy_pr(t); lazy_pr(t->l); lazy_pr(t->r);
t->first_elem = t->l ? t->l->first_elem : t->val;
t->last_elem = t->r ? t->r->last_elem : t->val;
//non-increasing and non-decreasing properties
bool lni=1, lnd=1, rni=1, rnd=1; //non-increasing/decreasing left and right subtrees
if(t->l){ //unite this value with left subtree
if(!t->l->non_incr || t->l->last_elem < t->val) lni=0;
if(!t->l->non_decr || t->l->last_elem > t->val) lnd=0;
}
if(t->r){ //with right subtree
if(!t->r->non_incr || t->r->first_elem > t->val) rni=0;
if(!t->r->non_decr || t->r->first_elem < t->val) rnd=0;
}
t->non_incr = lni&&rni, t->non_decr = lnd&&rnd;
}
void split(treap t, treap &l, treap &r, int pos, int tree_begin){
if(!t) return void(l=r=0);
lazy_pr(t);
int val_pos = tree_begin + get_size(t->l);
if(pos <= val_pos) split(t->l, l, t->l, pos, tree_begin), r=t;
else split(t->r, t->r, r, pos, val_pos+1), l=t;
recalc(l); recalc(r);
}
void merge(treap &t, treap l, treap r){
lazy_pr(l); lazy_pr(r);
if(!l || !r) t = l?l:r;
else if(l->heap_val > r->heap_val) merge(l->r,l->r,r), t=l;
else merge(r->l,l,r->l), t=r;
recalc(t);
}
void build(vector<int> &a){
for(int x:a) merge(root, root, new node(x));
}
int find_k(treap t, int tree_end){
lazy_pr(t);
if(!t || t->non_incr) return tree_end - get_size(t); //return position before this tree
int k = find_k(t->r, tree_end), val_pos = tree_end - get_size(t->r); //visit right subtree
if(!t->r || (k == val_pos && t->r->first_elem <= t->val)) k--; //check value of the root
lazy_pr(t->l);
if(t->l && k == val_pos-1 && t->l->last_elem >= t->val){
k = find_k(t->l, val_pos-1); //visit left subtree
}
return k;
}
int find_nln(treap t, int x, int tree_begin){
lazy_pr(t);
if(!t) return tree_begin;
if(t->val > x) return find_nln(t->l, x, tree_begin);
return find_nln(t->r, x, tree_begin + get_size(t->l)+1);
}
void next_p(int L, int R, treap t=root){
treap l, r, swap1, swap2, between;
split(t, t, r, R+1, 0);
int k = find_k(t, R)+1; //find LNIS
split(t, l, t, max(L,k), 0); //separate LNIS
t->reversed ^= 1;
if(k>L) { //if the subsegment isn't in non-increasing order
split(l, l, swap1, k-1, 0); //separate a_(k-1)
int nln = find_nln(t, swap1->val, k);
split(t, between, t, nln, k); split(t, swap2, t, nln+1, nln); //separate NLN
merge(t, swap1, t); merge(t, between, t); merge(t, swap2, t);
}
merge(t, l, t); merge(t, t, r);
}
Magic moment of professional
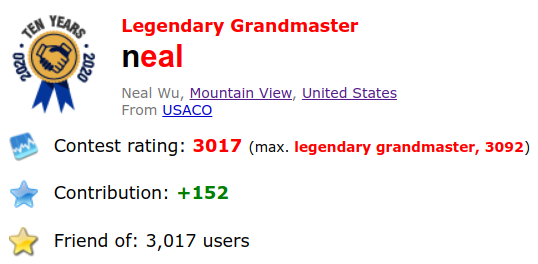
My magic moment
| Name |
|---|


