Today Deepmind published a blog post AI achieves silver-medal standard solving International Mathematical Olympiad problems.Deepminds model would have gotten 28 / 42 points from this years IMO (judged by "prominent mathematicians Prof Sir Timothy Gowers, an IMO gold medalist and Fields Medal winner, and Dr Joseph Myers, a two-time IMO gold medalist and Chair of the IMO 2024 Problem Selection Committee."). Some relevant notes from the post:
- "First, problems were manually translated into formal mathematical language for our systems to understand"
- "Our systems solved one problem within minutes and took up to three days to solve the others."
- "AlphaProof is a system that trains itself to prove mathematical statements in the formal language Lean. It couples a pre-trained language model with the AlphaZero reinforcement learning algorithm, which previously taught itself how to master the games of chess, shogi and Go."
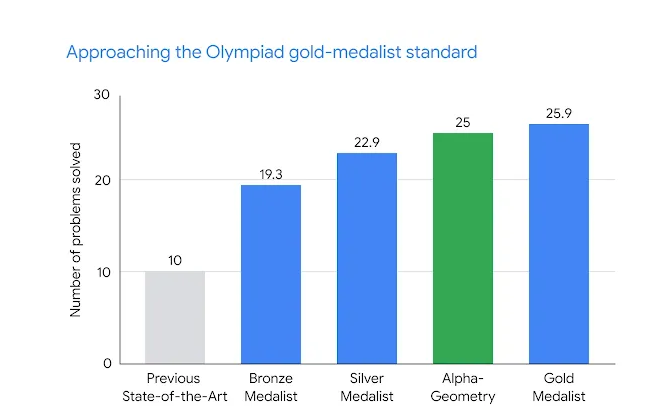
"Before this year’s competition, AlphaGeometry 2 could solve 83% of all historical IMO geometry problems from the past 25 years, compared to the 53% rate achieved by its predecessor." (Note: The AlphaGeometry paper was published in January)
- "AlphaGeometry 2 solved Problem 4 within 19 seconds after receiving its formalization".
I guess the question is: Will this scale?