Yesterday Deepmind published a paper about its new model AlphaGeometry. The model solved 25 out of 30 geometry problems from the IMOs 2000-2022. Previous SOTA solved 10 and average score of gold medalist was 25.9 on the same problems:
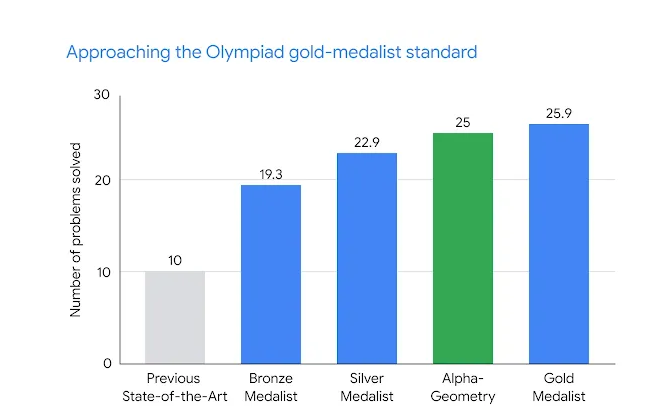
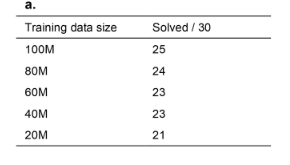
The model was trained only on synthetic data and it seems (to me) that more data would result in better results:
A notable thing is that AlphaGeometry uses an language model combined with a rule-bound deduction engine and solves problems with similar approach to humans.
The paper can be read here and the blog post can be found here
Own speculation:
I don't see any trivial reasons why similar strategy couldn't be used to other IMO areas (at least number theory and algebra) but I'm not an expert and haven't read all of the details. Generating a lot of data about for example inequalities or functional equations doesn't sound that much harder than generating data about geometry but again, I might be missing some important insight why good data is easy to generate about geometry. I'm not sure if this has direct implications on Competitive Programming AIs. Verifying proofs can be done automatically but I'm not sure if the same applies to algorithms. Still overall very interesting approach and results.











All geometry can be solved by coordinate bashing. I also feel like all geometry proofs are easier to formalize since they're not very complicated.
All geometry can be solved by coordinate bashing but the interesting thing is that AlphaGeometry didn't solve the problems by coordinate bashing: "It uses classical geometry rules with angles and similar triangles just as students do" (quote from Evan Chen)
Combinatorics >>>>>>>>>>>>>>>>>>>>>>>>>> euclidean G*ometry There's a proof that every problem stated in euclid's axioms can be solved using an algorithm, aka has a solution This isn't true for number theory
Does the fact that every problem stated in euclid's axioms can be solved using an algorithm help humans solve those problems?
To be clear, I agree that combinatorics is probably way harder for AIs than euclidean geometry.
Yeah that isn't really a big thing but every problem stated in euclid's axioms is guaranteed to have a solution, and also to be real any IMO geometry can just be coordinate bashed
I love geometry problems, but I can't solve them
I think the case of ad-hoc problems in CP are similar because quite a lot of them is reliant on discovering simple patterns from many examples with trial and error (while I admit that, due to the nature of ad-hoc itself, not all of them are such, I guess constructive problems might be outside of this scope)
MO Geometry also have a similar recipes, so I'm not too surprised that they are the first to be conquered among all. Actually I would say it came much later than I expected.
I think you're overestimating MO geometry problems. As I've pointed out earlier in the comments of the same blog as well as in earlier blogs, MO geometry specifically has a very small branching factor (in fact, I implied that if anything, they would be the first problems to be conquered by AI). This is why they are able to even generate their synthetic training data — the "syntax" and context of problems and solutions is very uniform. Meanwhile with ad-hoc problems (a.k.a. MO combinatorics), this seems to be much harder since at any stage you need to also do some analysis of the structure (in the sense that you can't spam theorems at them and expect them to work out of the box), which is not a major part of solving geometry problems for example, but making educated guesses is. Geometry also enjoys the advantage of having a relatively small number of axioms but with ad hoc problems you need to know a much larger set of things to solve them (mathematically, not from a human perspective). Similarly, the theory is already pretty deep in geometry, but it seems to be very scattered in ad-hoc problems (to give context, the amount of geometry theory we know is much more than chess theory, and I would say for reliably solving ad-hoc problems, you might even need something as wide as category theory to capture all of it). And about encoding patterns that you might get from trial and error in ad-hoc problems — it currently seems to be a hard problem to be able to come up with an general (and learnable) representation for them, meanwhile for geometry, it is not a big issue since the way most geometry problems are actually solved is not via trial and error, but by doing reasoning in the same way a search tree is generated.
As an aside, I've long believed that their symbolic approach is what will help AI do reasoning eventually (see my comments on the Meta AI paper under the same blog), and I'm glad that this is the direction AI researchers are taking and succeeding at.
I do think ad-hoc problems are harder than MO geometry for AI. I am just drawing a connection.
Oh, that wasn't very clear for me given your comments on that blog, and when you said "MO geometry also have similar recipes" I wanted to clarify that MO geo is much more systematic in how problems are approached (and much easier for machines). Thanks for clarifying!