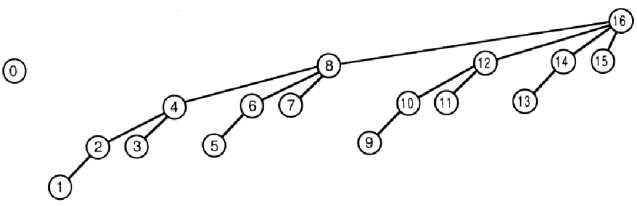
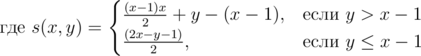As an addition to Teams going to ACM ICPC World Finals 2018 I suggest table below
Updated after Codeforces Round #474
Updated after Codeforces Round #475
| Team | Members | Rating(sum) |
|---|---|---|
| Peking University | Syloviaely, SkyDec, shanquan2 | 9172 |
| Moscow State University | LHiC, V--o_o--V, vintage_Vlad_Makeev | 8786 |
| Seoul National University | zigui, dotorya, molamola. | 8569 |
| University of Warsaw | Radewoosh, Errichto, mareksom | 8386 |
| St. Petersburg ITMO University | Belonogov, SpyCheese, izban | 8303 |
| Moscow Institute of Physics & Technology | Golovanov399, Kostroma, -imc- | 7909 |
| KAIST | ko_osaga, alex9801, Konijntje | 7709 |
| University of Tokyo | Hujiwara, hogloid, DEGwer | 7656 |
| University of New South Wales | JoeyWheeler, xxTastyHypeBeast666xx, AntiForest | 7635 |
| Tsinghua University | Stilwell, KFDong, xllend3 | 7624 |
| Fudan University | SakurakoujiRuna, tun, t90tank | 7604 |
| St. Petersburg State University | el_sanchez, Kaban-5, pavel.savchenkov | 7555 |
| Ural Federal University | kb., Tinsane, sivukhin | 7404 |
| University of Bucharest | alex.velea, bicsi, AndreiNet | 7401 |
| Sharif University of Technology | SeyedParsa, Deemo, M.Mahdi | 7191 |
| Uzhgorod National University | MrDindows, Melnyk, Rubanenko | 7166 |
| Saratov State University | BledDest, adedalic, Roms | 7120 |
| Massachusetts Institute of Technology | ksun48, desert97, cliu568 | 7072 |
| Shanghai Jiao Tong University | Akigeor, lbn187, Nisiyama_Suzune | 7062 |
| National Taiwan University | eddy1021, paulwang, akaiNeko | 7054 |
| Sharif University of Technology | Haghani, JeBeK, matrix | 6965 |
| Universidade de São Paulo | yancouto, victorsenam, arthur.nascimento | 6956 |
| The Chinese University of Hong Kong | nhho, hohomu, jasonyik | 6948 |
| National Research University Higher School of Economics | iskhakovt, kraskevich, Kronecker | 6881 |
| Scuola Normale Superiore | dario2994, Delfad0r, fram | 6877 |
| University of Electronic Science and Technology of China | Orenji.Sora, LaPlus, femsub | 6781 |
| Indian Institute of Technology — Roorkee | gvaibhav21, adkroxx, saharshluthra | 6768 |
| Ulsan National Institute of Science and Technology | Na2a, bekzhan29, nezametdinov | 6718 |
| Belarusian State University | 244mhq, Mediocrity, vilcheuski | 6707 |
| University of Tartu | oml1111, SLLN, .I. | 6707 |









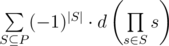
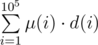
 функция Мёбиуса определяется так
функция Мёбиуса определяется так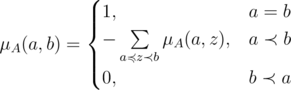
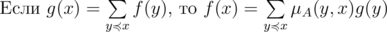
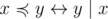 (строгий вариант
(строгий вариант 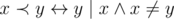 ). Например,
). Например, 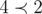 , а
, а 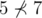 . Пусть
. Пусть 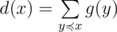
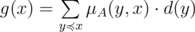
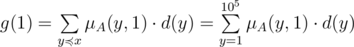
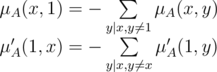
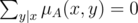
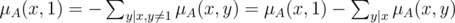 , следовательно,
, следовательно, 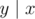 верно
верно 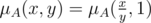
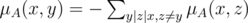 . Заметим, что
. Заметим, что 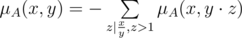
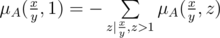
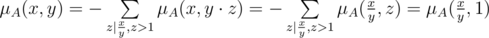
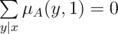
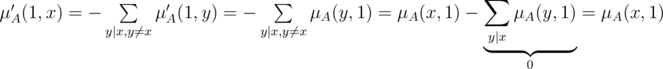
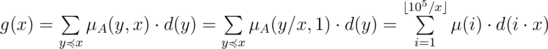
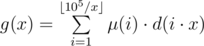
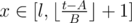 , что
, что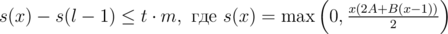
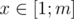 , что
, что