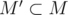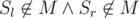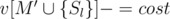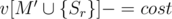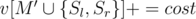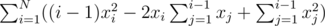Представляю полный разбор задач Codeforces Round #153. Если возникнут какие-то вопросы или пожелания -- пишите в комментариях, постараюсь ответить.
252A - Маленький xor (A div 2)
Переберем все отрезки чисел в массиве. Для каждого из них найдем xor и выберем тот отрезок, у которого xor максимальный. Осталось только вывести этот xor.
252B - Разупорядочивание массива (B div 2)
Если все числа в массиве равны между собой, то искомой пары позиций не существует. Теперь предположим, что в массиве есть хотя бы 2 различных числа. Будем перебирать все пары различных чисел и для каждой такой пары попробуем поменять местами числа на этих позициях, после чего проверим, является ли массив отсортированным и в случае необходимости, выведем ответ. Если этот алгоритм не нашел нужной пары позиций, то выведем -1.
Кажется, что этот алгоритм работает за O(N3). На самом деле это не так и его время работы можно оценить как O(N). Дело в том, что если есть хотя бы 3 пары позиций с различными числами, то одна из них обязательно подойдет. Это связано с тем фактом, что всего существует 2 различных отсортированных массива (по убыванию и по возрастанию), а все пары позиций с различными числами после обмена дают различные массивы. Следовательно, один из трех различных массивов обязательно будет не отсортированным.
252C - Точки на прямой (C div 2)
251A - Точки на прямой (A div 1)
Переберем правую точку из тройки, при этом будем поддерживать указатель на самую левую точку, которая отстоит от текущей на расстояние не большее, чем d. Мы легко можем определить количество точек внутри отрезка между двумя указателями (не включая правую точку). Обозначим это количество через k. Тогда ясно, что существует ровно k * (k - 1) / 2 троек точек, в которых самая правая точка совпадает с текущей, которую мы перебираем. Осталось просуммировать ответы для всех таких точек.
252D - Игра с перестановками (D div 2)
251B - Игра с перестановками (B div 1)
В начале проверим, совпадает ли перестановка s с тождественной. Если совпадает, то ответ "NO".
Теперь приведем алгоритм, который работает во всех случаях, кроме одного. О нем будет сказано позже. Будем применять прямую перестановку (в условии она обозначается как q) до тех пор, пока текущая перестановка не совпадет с s, либо пока мы не сделаем k шагов. Если текущая перестановка совпала с s, то посмотрим на количество ходов, которые мы уже сделали (обозначим его через t). Если число k - t четное, то мы можем выбрать любую перестановку в нашей последовательности, кроме предпоследней и применять к ней (k - t) / 2 раз связку "обратная перестановка + прямая перестановка". Это можно не выполнять явно, просто достаточно проверить четность числа k - t. Итак, если оно четное, то ответ "YES".
Аналогично, попробуем применять обратную к q перестановку до тех пор, пока мы не получим перестановку s, либо пока не сделаем k шагов. И опять, если мы получили перестановку s, то проверим четность оставшегося количества ходов и в случае, если это количество четно -- выведем "YES". Можно понять, что в противном случае ответ "NO".
Приведенный выше алгоритм работает для всех случаев, кроме одного: когда перестановка q совпадает со своей обратной перестановкой, причем перестановка s достижима за один ход. В этом случае, если k = 1, то ответ "YES", иначе ответ "NO".
Полученный алгоритм работает за время O(N2).
252E - Превращение числа (E div 2)
251C - Превращение числа (C div 1)
Обозначим через L наименьшее общее кратное всех чисел от 2 до k. Заметим, что если a кратно L, то мы не сможем уменьшить его операцией второго типа. А это значит, что в оптимальной последовательности превращений будут присутствовать все числа, кратные L, которые находятся между b и a. Разобьем все числа от b до a на отрезки между числами, кратными L. Может выйти так, что первый и последний отрезки будут не полными. Видно, что достаточно решить задачу для первого и последнего отрезка, а также решить задачу для любого отрезка между ними, после чего последний результат нужно еще умножить на количество отрезков между крайними. Осталось только сложить полученные 3 числа и вывести ответ.
Также требовалось аккуратно рассмотреть случаи, когда у нас есть всего 1 или 2 отрезка.
Сложность решения O(L).
251D - Два множества (D div 1)
Обозначим xor всех чисел через X. Также, обозначим xor всех чисел в искомом первом наборе через X1, а во втором наборе -- через X2. Заметим, что если i-й бит в числе X равен единице, то i-е биты в числах X1 и X2 равны либо 0 и 1, либо 1 и 0, соответственно. Аналогично, если i-й бит в числе X равен нулю, то i-е биты в числах X1 и X2 равны 1 и 1, либо 0 и 0, соответственно. Как видим, на сумму X1 + X2 влияют только те биты, которые в числе X равны нулю. Пока забудем про то, что от нас требуется минимизировать число X1 и найдем максимальную возможную сумму X1 + X2.
Для того чтобы найти X1 + X2 сделаем еще одно наблюдение. Рассмотрим старший бит числа X, который равен нулю. Если существуют такие разбиения исходного набора на два, в котором этот бит равен единице в числе X1, то оптимальное разбиение обязательно должно быть одним из них. Чтобы доказать это, вспомним что соответствующий бит в числе X2 также равен единице. Обозначим соответствующую этому биту степень двойки через L. Тогда, если в числах X1 и X2 этот бит равен единице, то даже в том случае, когда все остальные биты равны нулю, сумма X1 + X2 равна 2L + 1. Если же в рассматриваемый бит мы в X1 и X2 поставим ноли, то даже в случае, когда все остальные биты равны единице, сумма X1 + X2 будет равна 2L + 1 - 2, что меньше, чем 2L + 1. Утверждение доказано.
Будем решать задачу при помощи жадного алгоритма. Переберем все биты, которые в числе X равны нулю, начиная со старшего. Попробуем поставить в число X1 на эту позицию единицу и проверим, существует ли хотя бы одно разбиение, которое удовлетворяет этому условию и всем уже поставленным условиям для предыдущих бит. Если такое разбиение существует, то оставляем это условие и переходим к младшим битам. Если же ни одного такого разбиения не существует, то переходим к младшим битам, не добавляя никаких новых условий.
Итак, для набора условий осталось научиться проверять, существует ли хотя бы одно разбиение, которое удовлетворяет всем этим условиям. Для каждого условия на бит с номером i составим уравнение над полем Z2 с n неизвестными, в котором коэффициент при каждой переменной равен i-му битчисла с соответствующим ей номером. Если неизвестная равна единице, то соответствующее число мы берем в первое множество, иначе -- во второе. Полученную систему уравнений можно решить алгоритмом Гаусса. Заметим, что нам не нужно каждый раз при добавлении нового уравнения решать всю систему с нуля. Достаточно лишь за O(NK) пересчитать матрицу из предыдущего состояния. Здесь, K -- количество уравнений в системе.
Итак, мы научились находить разбиение с максимальной суммой X1 + X2. Минимизировать X1 можно аналогичным образом: будем идти по всем битам, которые равны единице в числе X, начиная со старшего. Для очередного бита будем пытаться поставить в число X1 ноль. Если после этого система уравнений перестала иметь решение, то в соответствующем бите ставим единицу, иначе -- оставляем ноль и переходим дальше.
Сложность полученного алгоритма равна O(NL2), где L -- битовая длина максимального из чисел. Для дальнейшего ускорения можно использовать структуру bitset в алгоритме Гаусса, хотя этого не требовалось для получения Accepted на контесте.
251E - Дерево и таблица (E div 1)
Если N = 1, то существует ровно 2 укладки дерева на таблицу.
Если в дереве есть вершина, степень которой превышает 3, то ответ 0. Это связано с тем, что любая клетка таблицы имеет не более трех соседей.
Если в дереве нет вершин степени 3, то ответ 2 * n2 - 2 * n + 4. Эта формула выводится естественным образом при дальнейшем решении задачи. Также, можно было написать простую динамику для решения задачи в случае, когда у всех вершин степень 1 или 2. Так или иначе, давайте докажем приведенную формулу.
Для начала, решим немного другую задачу, которая будет использоваться при решении основного случая. Найдем количество способов уложить дерево на таблицу при условии, что в дереве нет вершин степени 3, а также одна вершина степени 1 прикреплена к левому верхнему углу таблицы (будем считать, что это вершина номер 1). Можно показать, что если размер таблицы 2xK, то количество способов укладки дерева равно K. Доказывать это будем по индукции. Для K = 1 утверждение, очевидно, выполняется. Для K > 1 будем доказывать следующим образом. Предположим, что таблица ориентирована горизонтально, т.е. у нее 2 строки и K столбцов. Если вершину, соседнюю с первой, мы поставим правее от нее, то потом у нас есть только один способ расположения дерева. Если же мы поставим ее снизу от первой, то следующую вершину мы обязаны поставить правее от нее, т.е. в клетку (2, 2). Теперь, мы получили ту же задачу, только K стало на единицу меньше. Таким образом, мы получили рекуррентное соотношение: f(K) = f(K - 1) + 1 и начальное условие f(1) = 1. Легко видеть, что в этом случае f(K) = K.
Итак, теперь вернемся к исходной задаче: сколько существует способов расположить дерево без вершин степени 3 на таблице 2xN. Без ограничения общности, предположим, что первая вершина дерева имеет степень 1. Будем рассматривать только те варианты, в которых первая вершина лежит на верхней строке таблицы, после чего просто умножим ответ на 2. Итак, если первая вершина лежит в первом или последнем столбце, то, как мы уже выяснили, существует N способов расположить на таблице оставшееся дерево. Если же первая вершина лежит в столбце с номером i (нумерация начинается с единицы, левый столбец имеет номер 1), то существует i - 1 способ, в котором соседняя с первой вершина лежит справа от нее. Также, существует N - i способов, в которых соседняя с первой вершина лежит слева от нее. Просуммировав это для всех столбцов и умножив ответ на 2, получим окончательный результат: 2 * n2 - 2 * n + 4.
Итак, остался самый главный случай, когда в дереве есть вершина степени 3. Объявим такую вершину корнем и подвесим дерево за него. Если существует несколько вершин степени 3, то в качестве корня мы можем выбрать любую из них. Предположим, что корень лежит в первой строке таблицы, а потом просто умножим ответ на 2. Ясно, что корень будет лежать на клетке, имеющей трех соседей. Переберем, какой из потомков корня будет лежать слева от него, какой будет лежать снизу, а какой -- справа. В случае, если потомок, лежащий снизу от корня, имеет степень 2 или 3, нам нужно еще перебрать, какой из его детей пойдет влево, а какой -- вправо. Всего есть не более 12 вариантов расположения потомков корня и потомков его "нижнего" сына. Итак, теперь у нас занят весь столбец, в котором лежит корень, а значит, как бы мы ни укладывали дерево дальше, все вершины, лежащие справа от корня там и останутся лежать. Аналогично, все вершины, лежащие слева от корня, там и останутся. Мало того, у нас есть фиксированное количество вершин слева и справа от корня, а значит, у нас есть ровно один вариант его расположения на таблице. Заметим, что если слева от корня находится нечетное количество вершин, то дальше дерево мы уложить не сможем. Посчитать количество вершин можно, просто сложив размеры поддеревьев для его потомка, а также потомка его "нижнего" сына, которые находятся слева от корня.
Итак, у нас есть 2 независимые подзадачи и нам нужно для каждой из них посчитать количество способов уложить дерево в таблице. При этом, у нас возможны только 2 ситуации:
1) Нам нужно уложить поддерево с корнем в вершине v на прямоугольную таблицу, причем вершина v находится в углу таблицы (для определенности будем считать, что это левый верхний угол).
2) Нам нужно уложить поддеревья с корнями в вершинах v1 и v2 на прямоугольную таблицу, причем вершина v1 находится в левом верхнем углу таблицы, а вершина v2 -- в левом нижнем.
Очевидно, что любая из этих двух задач имеет ненулевой ответ только в том случае, когда суммарный размер соответствующих поддеревьев -- четный.
Покажем, как свести задачу второго типа к задаче первого типа. Итак, если у вершины v1 или v2 есть 2 потомка, то ответ 0. Если у них по одному потомку, то мы можем перейти в них и получить ту же самую задачу. Если у обоих вершин нет потомков, то мы уже покрыли всю таблицу, так что ответ на задачу равен 1. Если же у одной вершины нет потомка, а у второй вершины один потомок, то мы получили задачу первого типа для этого потомка.
Итак, нам осталось решить задачу первого типа. Обозначим через f(v) количество способов уложить поддерево с корнем в вершине v на прямоугольную таблицу. Размер этой таблицы однозначно определяется из размера поддерева. Для решения задачи нам нужно рассмотреть 2 случая:
а) Вершина v имеет степень 2.
б) Вершина v имеет степень 3.
В случае, если вершина v имеет степень 2 и в ее поддереве нет ни одной вершины степени 3, то f(v) = s(v) / 2, где s(v) -- размер поддерева с корнем в вершине v. Ранее мы уже доказывали эту формулу. Теперь, предположим что в поддереве вершины v есть хотя бы одна вершина степени 3. Если таких вершин несколько, выберем ту, которая ближе всего к v. Обозначим ее через w. Итак, есть 2 варианта:
а.1) Путь из вершины v в вершину w пойдет так, что предпоследняя вершина в пути лежит слева от w.
а.2) Путь из вершині v в вершину w пойдет так, что предпоследняя вершина в пути лежит сверху от w.
Третьего варианта нет, поскольку у вершины w степень 3, а если мы "обойдем" ее так, чтобы предпоследняя вершина на пути лежала справа от w, то при этом клетка над w также будет занята, что сделает невозможным правильное расположение всех соседей вершины w.
В каждом из вариантов а.1) и а.2) переберем, куда идут потомки вершины w (одно направление уже занято ее предком, так что остается ровно 2 свободных направления). В случае, если потомок степени >1 идет вниз, требуется также перебрать, куда идут какие его потомки (есть 2 варианта: вправо и влево). После этого, справа от вершины w опять получается задача типа 1) или 2), которые были сформулированы выше. Слева от вершины w у нас есть дерево либо не укладывается вообще, либо укладывается однозначно. Это можно проверить исходя из длины пути из v в w, а также размера поддерева внука вершины w, который пошел в тот же столбец, что и w (если такой внук вообще есть). Осталось просуммировать ответы для всех этих вариантов.
Итак, задачу типа а), когда вершина v имеет степень 2, мы решать уже умеем. Осталось решить задачу б), когда вершина v имеет степень 3. Для этого достаточно перебрать, какой из ее потомков пойдет вправо, а какой — вниз. После этого получаем задачу либо типа 1), либо типа 2), которые были сформулированы выше.
Итоговая сложнось решения O(N).









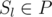 или
или 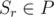 , то, очевидно, эти позиции рядом никогда не будут. Отсюда можно сделать вывод, что для фиксированного
, то, очевидно, эти позиции рядом никогда не будут. Отсюда можно сделать вывод, что для фиксированного